세그먼트 트리(Segment Tree)
세그먼트 트리(Segment Tree)는 배열 간격에 대한 정보를 이진 트리에 저장하는 자료구조입니다.
다음 예를 보겠습니다.
A = {1, 2, 3, 4, 5 … ,N} 라는 배열에 아래 연산을 M번 수행한다고 생각해봅시다.
- 배열의 범위 합을 구하는 Query 연산
- A[0] + A[1] + A[2] + … + A[N-1]
- i번째 배열 값을 v로 변경하는 Update 연산
- A[i] = v
단순한 방법으로는 각각 배열에 접근하여 연산을 한다면 시간 복잡도는 1번 연산 O(N), 2번 연산 O(1)이 됩니다.
이 두 연산을 M번 수행한다면 총 시간 복잡도는 O(MN)+O(M) = O(MN)이 됩니다.
세그먼트 트리를 사용하면 범위 최소/최대 및 합계 Query 및 범위 Update를 O(logN) 시간에 해결할 수 있습니다.
위 두 연산에 세그먼트 트리를 사용한다면 O(MlogN) + O(MlogN) = O(MlogN) 시간으로 개선시킬 수 있습니다.
세그먼트 트리 구성
세그먼트 트리는 이진트리이므로 간단한 선형 배열을 사용하여 나타낼 수 있습니다.
부모 노드의 인덱스가 i라면 2i은 왼쪽 자식 노드이고 2i+1은 오른쪽 자식 노드입니다.
세그먼트 트리의 각 노드에는 구간 정보가 저장되어 있습니다.
예) 구간 합, 구간 최대/최소 값
다음은 배열 A = {1,2,3,4,5} 에 대한 세그먼트 트리를 시각화한 그림입니다.
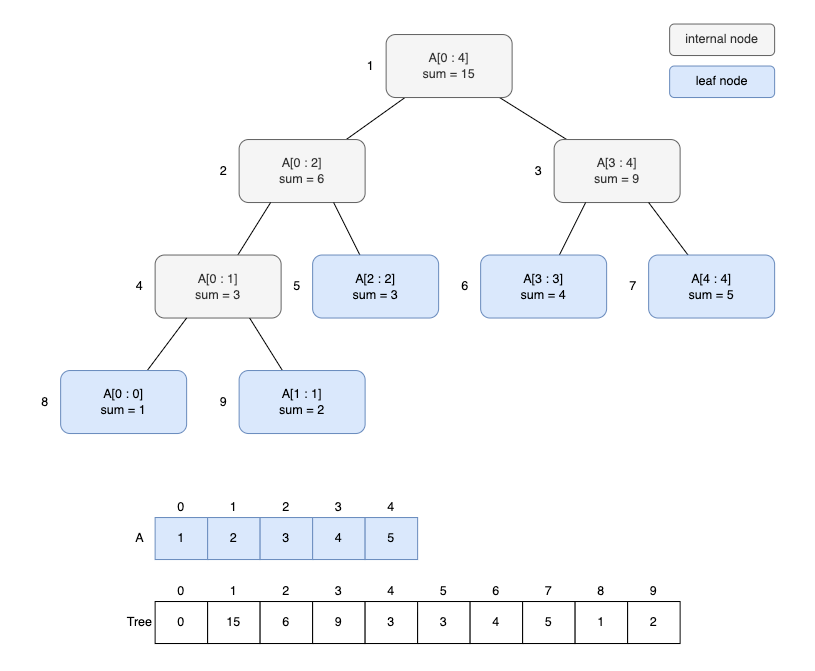
각 노드에는 배열의 구간 합이 저장되어 있습니다.
리프 노드에는 주어진 배열(A) 값들이 저장되고 내부 노드에는 자식 노드의 합이 저장됩니다.
세그먼트 트리 구현
세그먼트 트리에는 세 가지(Build, Query, Update) 작업이 있습니다.
여기서는 구간 합 정보를 저장하는 세그먼트 트리를 구현하는 방법을 알아보겠습니다.
세그먼트 트리는 전 이진트리(Full Binary Tree)입니다.
그렇기 때문에 크기가 n인 배열을 가지고 리프 노드가 n개인 세그먼트 트리를 만들 때 필요한 노드 수는 다음과 같습니다.
$$ 1 + 2 + 4 + \dots + 2^{\lceil\log_2 n\rceil} \lt 2^{\lceil\log_2 n\rceil +1} \lt 4n $$
높이가 \( h = \lceil\log_2 n\rceil \) 라면
필요한 배열 크기는 \( 2^{(h+1)} - 1 \) 이며 편의를 위해 \( 2^{(h+1)} \) 또는 \( 4n \)으로 크기를 정하기도 합니다.
from math import ceil, log2
height = ceil(log2(n))
tree_size = 1 << (height+1)
tree = [0] * tree_size
# or
tree_size = 4 * n
tree = [0] * tree_size
Build
세그먼트 트리를 만드는 작업을 합니다.
구현은 다음과 같습니다.
- 세그먼트 트리는 재귀를 사용하여 구축할 수 있습니다.
- 트리를 순회하며 작업을 진행합니다.
- 리프 노드라면 배열(A)의 요소를 저장합니다.
- 내부 노드라면 구간 정보를 저장합니다. (예를 들어 구간 정보가 구간 합이라면 두 자식 노드의 합을 저장합니다.)
구현
- 여기서 start, end는 배열 A에 대한 범위입니다.
def build(node, start, end):
if start == end:
# 리프 노드라면 원소를 저장한다.
tree[node] = A[start]
return
mid = (start + end) // 2
# 왼쪽 자식으로 재귀
build(node*2, start, mid)
# 오른쪽 자식으로 재귀
build(node*2+1, mid+1, end)
# 내부 노드라면 두 자식 노드의 합을 저장한다.
tree[node] = tree[node*2] + tree[node*2+1]
return
Query
세그먼트 트리에서 구간 정보를 가져옵니다.
구현은 다음과 같습니다.
- 트리를 순회합니다.
- 노드가 나타내는 범위가 지정된 범위 밖에 있다면 0을 반환합니다.
- 노드가 나타내는 범위가 지정된 범위 내에 있다면 값을 반환합니다.
- 노드가 나타내는 범위가 지정된 범위 일부만 포함한다면 왼쪽 자식과 오른쪽 자식의 합을 반환합니다.
예를 들어 배열 A = {1,2,3,4,5}에서 2부터 4까지 구간 합을 구한다면 아래 그림처럼 컬러 노드들을 방문하게 되고 그중 초록색 노드 값을 사용하여 결과를 반환하게 됩니다. (3+ 9 = 12)
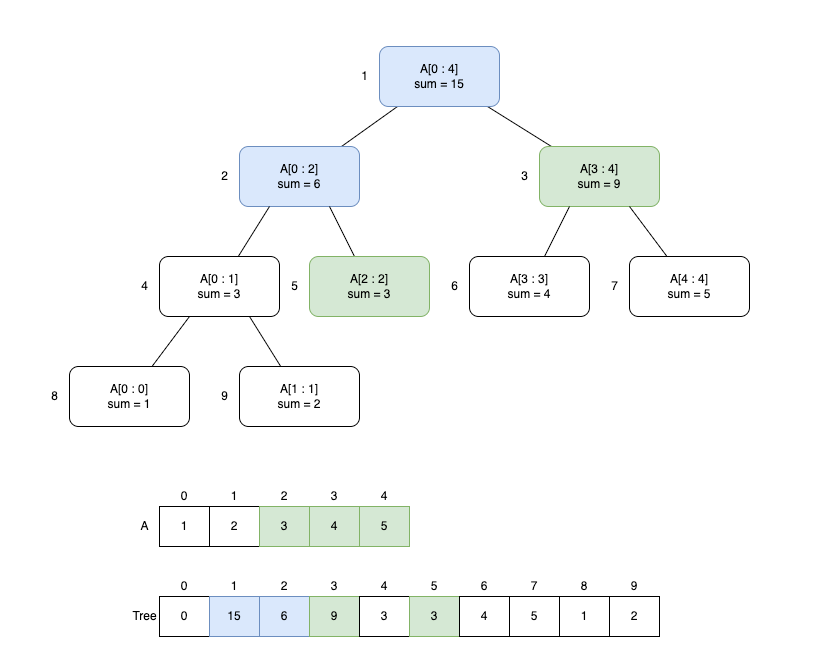
구현
- 여기서 노드가 나타내는 범위는 start, end이고 지정된 범위는 left, right입니다.
- 위 그림에서 지정된 범위는 left = 2, right = 4가 됩니다.
def query(node, start, end, left, right):
if right < start or end < left:
# 노드가 지정된 범위 밖에 있는 경우
return 0
if left <= start and end <= right:
# 노드가 지정된 범위 안에 있는 경우
return tree[node]
# 노드가 지정된 범위 일부에 있는 경우
mid = (start + end)//2
left_child = query(node*2, start, mid, left, right)
right_child = query(node*2+1, mid+1, end, left, right)
return left_child + right_child
Update
index번째 배열 A를 var값으로 변경하는 작업을 합니다. (A[index] = var)
update는 index가 포함된 구간을 담당하는 노드들만 변경합니다.
예를 들어 A = {1,2,3,4,5} 배열에서 A[2] = 5로 변경할 때, 변경해야 하는 구간은 다음과 같습니다. 색깔 노드는 방문하여 변경하는 노드입니다.
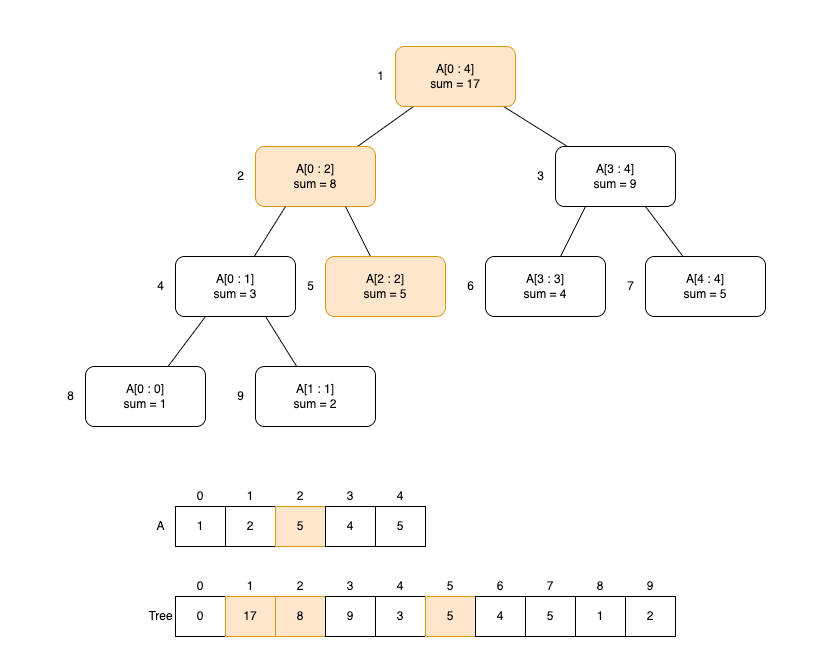
구현은 다음과 같습니다.
- 트리를 순회합니다.
- index가 포함된 구간을 가지고 있는 자식 노드로 재귀합니다.
- 리프 노드라면 배열 값을 변경합니다.
- 내부 노드라면 구간 정보를 저장합니다. (예를 들어 구간 정보가 구간 합이라면 두 자식 노드의 합을 저장합니다.)
def update(node, start, end, index, val):
if start == end:
# 리프 노드라면 배열 값을 변경한다.
tree[node] = val
return
mid = (start + end) // 2
# index가 포함된 구간을 가진 자식 노드로 재귀한다.
if start <= index and index <= mid:
update(2*node, start, mid, index, val)
else:
updaet(2*node+1, mid+1, end, index, val)
# 내부 노드라면 두 자식 노드의 합을 저장한다.
tree[node] = tree[node*2] + tree[node*2+1]
return
변화량을 사용한 구현
- 변화량(diff)을 사용하여 업데이트하는 방법도 있습니다.
- index 번째 배열 A를 val값으로 변경할 때 변화량은 diff = val - A[index]가 됩니다.
- index가 포함된 구간을 가진 노드들만 diff만큼 증가시키는 방식으로 구현합니다.
예를 들어 A = {1,2,3,4,5} 배열에서 A[2] = 5로 변경할 때, diff는 5 - 3 = 2가 되고 아래 색깔 노드만 diff만큼 증가시키면 됩니다.
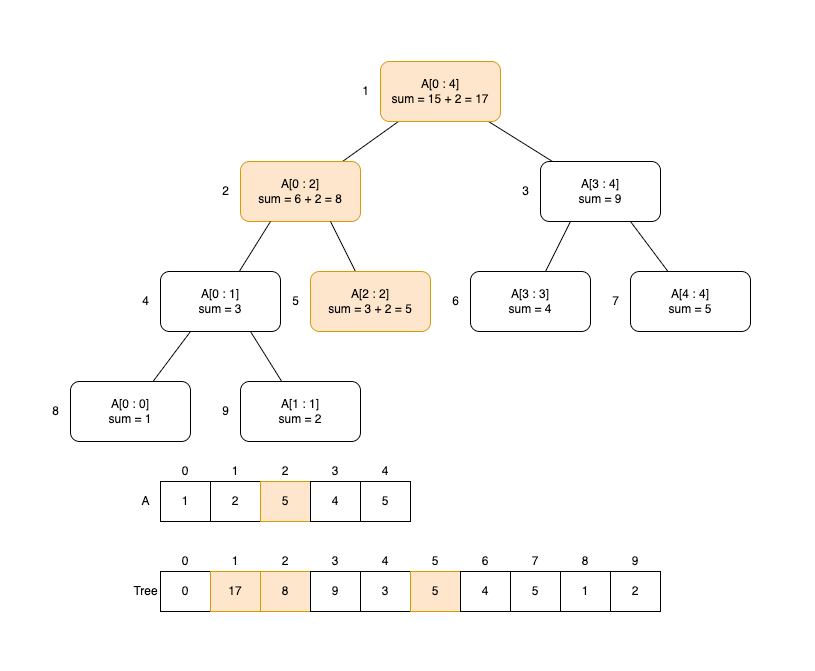
def update(node, start, end, index, diff):
if index < start or end < index:
#index가 노드 범위 밖이면 탐색을 중단한다.
return
# 노드를 diff 만큼 증가시킨다.
tree[node] += diff
if start != end:
# 리프 노드가 아닌 경우 자식 노드를 update해준다.
mid = (start + end) // 2
update(node*2, start, mid, index, diff)
update(node*2+1, mid+1, end, index, diff)
return




