서로소 집합(Disjoint Set) & 유니온 파인드(Union find)
서로소 집합(Disjoint Set)
Disjoint Set(서로소 집합, 분리 집합)이란 서로 공통된 원소를 가지고 있지 않은 두 개 이상의 집합을 말합니다.
Disjoint set 자료구조를 사용하면 서로 다른 원소들이 같은 집합에 속해있는지, 혹은 속해있지 않은지를 판별하는 데에 유용하게 사용할 수 있습니다.
Disjoint set 자료구조는 MakeSet, Union, Find라는 연산을 제공합니다.
MakeSet
MakeSet 연산은 주어진 요소만 포함하는 집합을 생성합니다.
이 연산에서 parent 배열을 생성합니다.
parent 배열은 노드의 부모 노드를 저장하고 있습니다. 부모 노드가 없다면 자기 자신을 가리킵니다.
이 배열은 union, find 연산에서 사용됩니다.

# MakeSet
parent = [i for _ in range(n)] # n is node countFind
Find 연산은 어떤 원소가 주어졌을 때 이 원소가 속한 집합의 대표 원소(=루트 노드)를 반환하는 연산입니다.
이 연산은 대표 원소에 도달할 때까지 부모 배열을 재귀적으로 순회합니다.
초기 find 연산은 자기 자신을 가리킵니다. Find(i) = i
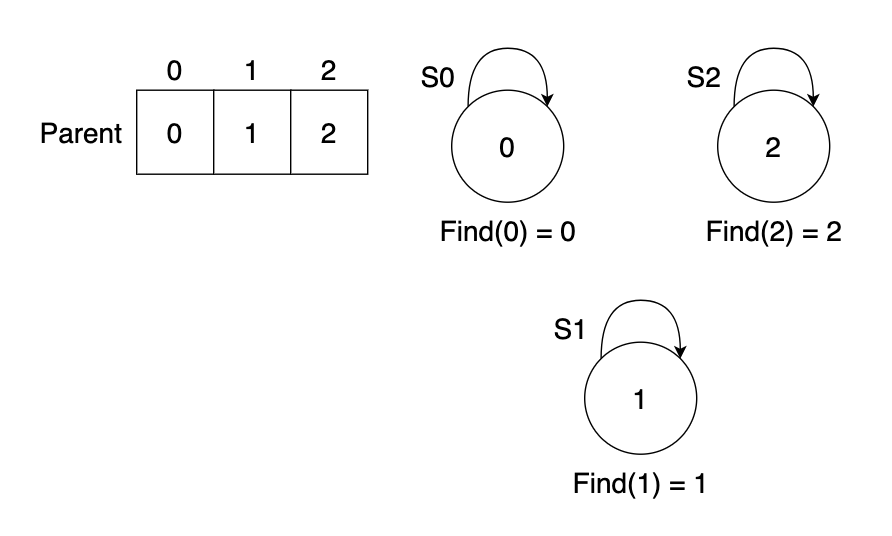
병합된 집합이 있다면 그 집합의 대표 원소(=루트 노드)를 반환합니다.

def find(x):
if x == parent[x]:
return x
return find(parent[x])Union
두 개의 집합을 하나의 집합으로 합치는 연산입니다. 즉, 한 트리의 루트를 다른 트리의 루트에 연결하여 두 트리를 하나로 결합합니다.
Union 과정은 다음과 같습니다.
- find 연산을 통해 두 요소의 루트 노드를 찾음.
- 두 루트 노드중 하나를 다른 트리의 루트 노드 아래에 배치하여 두 트리를 합침.

def union(a, b):
a = find(a)
b = find(b)
parent[b] = a
두 트리를 합치는 과정에서 최악에 경우 선형 트리가 생길 수 있습니다.

이 경우 Find 연산은 O(N)의 시간이 걸리게 되며 Union 또한 Find연산을 사용하기 때문에 O(N)의 시간이 걸리게 됩니다.
개선
union과 find 연산의 성능은 트리의 높이에 크게 의존합니다. 성능을 높이려면 트리의 높이를 최소화해야 합니다.
트리의 높이를 최소화하기 위해 다음과 같은 2가지 방법이 있습니다.
경로 압축 (Path Compression)
find 연산을 수행할 때마다 트리의 구조를 평평하게 만드는 방법입니다.
이 방법은 루트 노드까지 순회중 방문한 각 노드들이 직접 루트 노드를 가리키도록 하여 모든 노드들은 같은 대표 노드를 공유하게 됩니다.
평평한 트리가 만들어진 이후에는 O(1)만에 find를 수행할 수 있습니다.

def find(x):
if x == parent[x]:
return x
parent[x] = find(parent[x])
return parent[x]유니온 바이 랭크(Union by rank)
이 방법은 항상 작은 트리를 큰 트리 루트에 붙이는 방법입니다. 여기서 작은 트리는 상대적으로 높이가 낮거나 사이즈가 작은 트리를 의미합니다.
이 방법에서는 rank라는 배열을 사용합니다. rank배열에는 트리의 높이 or 사이즈가 저장됩니다.

Union by size
rank 배열에 트리의 사이즈(= 노드 수)를 저장합니다. union시 노드수가 작은 트리를 큰 트리에 합칩니다.
# union by size
rank = [1 for _ in range(n)]
def union(a, b):
a = find(a)
b = find(b)
if rank[a] < rank[b]:
a, b = b, a # swap
parent[b] = a
rank[a] += rank[b]Union by height
rank 배열에 트리의 높이를 저장합니다. union시 높이가 낮은 트리를 높은 트리에 합칩니다.
# union by height
rank = [1 for _ in range(n)]
def union(a, b):
a = find(a)
b = find(b)
if rank[a] < rank[b]:
a, b = b, a # swap
parent[b] = a
if rank[a] == rank[b]:
rank[a] += 1
union-find 연산은 최악의 경우 O(N) 시간이 걸립니다. 여기서 N은 노드의 수입니다.
이 방법은 union by rank와 경로 압축을 사용하면 O(logN)으로 개선할 수 있습니다.
union-find 연산은 주로 크루스칼 알고리즘(Kruskal’s Algorithm)을 구현할 때나 그래프 사이클을 탐지할 때 사용됩니다.




