그래프 표현 및 구현
그래프는 일반적으로 두 가지 방식으로 표현합니다.
- 인접 행렬 (adjacency matrix)
- 인접 리스트 (adjacency list)
인접 행렬(adjacency matrix)
인접 행렬은 그래프를 2차원 배열에 저장하는 방법입니다.
부속된 간선을 찾는 것은 빠르지만 |V| x |V| 만큼의 공간이 필요하여 저장 측면에서 비효율적입니다. (|V| : 정점 수)
노드 수보다 간선 수가 많은 dense graph이거나 빠르게 부속(incident)된 간선을 찾을 때 주로 사용합니다.
각 행과 열은 정점을 나타냅니다.
1. 방향성 그래프 (Directed Graph)
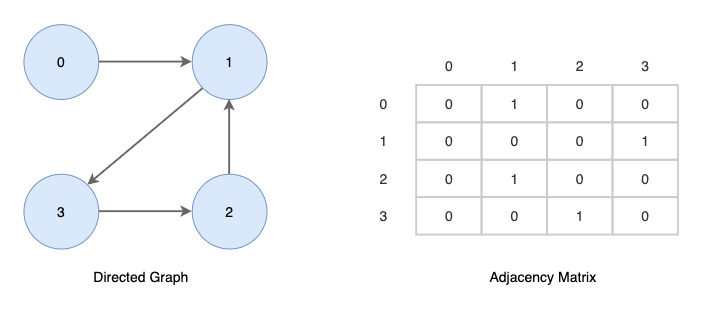
방향성 그래프를 인접행렬로 표현하면 다음과 같습니다.
각 정점이 인접하다면 1을 저장하고 그렇지 않다면 0을 저장합니다.
2. 무방향성 그래프 (Undirected Graph)
무방향성 그래프를 인접행렬로 표현하면 다음과 같습니다.
각 정점이 인접하다면 1을 저장하고 그렇지 않다면 0을 저장합니다.
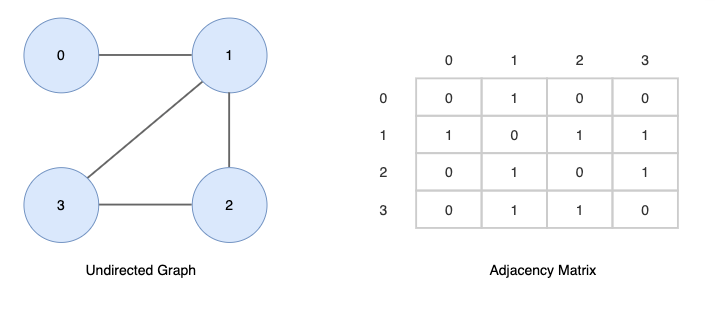
정점 u와 v사이의 간선은 arr[u][v], arr[v][u] 모두 1로 표현하기 때문에 대칭 행렬이 된다는 특징이 있습니다.
이 특징을 이용하여 시간을 절약하기 위해 대칭행렬의 절반만 처리하도록 할 수도 있습니다.
3. 가중치 그래프(Weighted Graph)
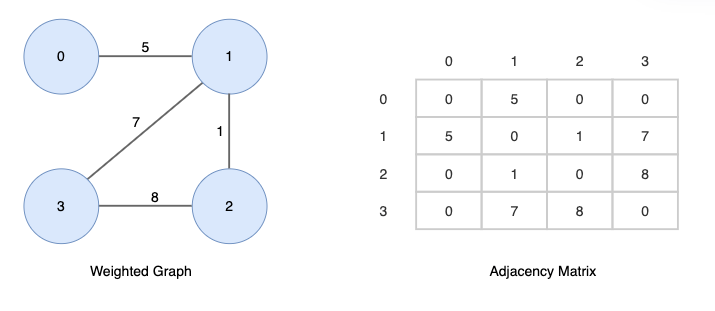
가중치 그래프를 인접행렬로 표현하면 다음과 같습니다.
각 정점이 인접하다면 간선의 가중치를 저장하고 그렇지 않다면 0을 저장합니다.
가중치가 0인 경우와 대비하기 위해 ∞로 표시하기도 합니다.
구현
무방향 그래프를 생성하고 간선을 추가하는 코드입니다.
typedef struct Graph {
int vertexNumber;
int** adj; // 2차원 배열을 저장하기 위한 공간
} Graph;
// n개의 정점을 가진 Grpah를 만든다.
Graph* createGraph(int n) {
int i,j = 0;
Graph *G = NULL;
G = (Graph*)malloc(sizeof(Graph));
G->vertexNumber = n;
G->adj = malloc(sizeof(int*) * n);
for (i = 0; i < n; i++) {
G->adj[i] = malloc(sizeof(int) * n);
}
// 그래프 초기화
for (i=0; i < n; i++) {
for (j=0; j < n; j++) {
G->adj[i][j] = 0;
}
}
return G;
}
// 무방향그래프에 대한 새로운 간선을 추가한다.
void addEdge (Graph* g, int v, int w) {
g->adj[v][w] = 1;
g->adj[w][v] = 1;
}
void printGraph (Graph* g) {
int i,j = 0;
for (i=0; i < g->vertexNumber; i++) {
for (j=0; j < g->vertexNumber; j++) {
printf("%d ", g->adj[i][j]);
}
printf("\n");
}
}
void main (void) {
Graph *g = NULL;
g= createGraph(4);
addEdge(g,0,1);
addEdge(g,1,2);
addEdge(g,1,3);
addEdge(g,2,3);
printGraph(g);
}Output:
0 1 0 0
1 0 1 1
0 1 0 1
0 1 1 0
시간 복잡도 (Time Complexity) & 공간 복잡도 (Space Complexity)
시간 복잡도
- 어느 두 정점(i, j)에 부속된 간선이 있는지 체크하는 연산
- O(1)
- 인접행렬 i행 j열을 참조하면 되기 때문입니다.
- 임의의 한 정점(i)에 인접한 정점을 찾는 연산
- O(|V|)
- 인접행렬에서 i행 전체에 대해 조사하면 되기 때문입니다.
공간 복잡도
- O(\(|V^2|\))
- 노드수 x 노드수 만큼의 행렬이 필요하기 때문입니다.
인접 리스트(adjacency list)
인접 리스트는 인접한 정점을 연결 리스트로 저장하는 방법입니다.
인접 리스트는 연결된 간선에 대한 값만 저장하기 때문에 저장 측면에서 효율적이고 간선 수보다 노드 수가 많은 spare graph에 주로 사용합니다.
정점은 배열로 저장하고 각 정점에 인접한 정점들은 연결 리스트로 관리합니다.
1. 방향성 그래프 (Directed Graph)
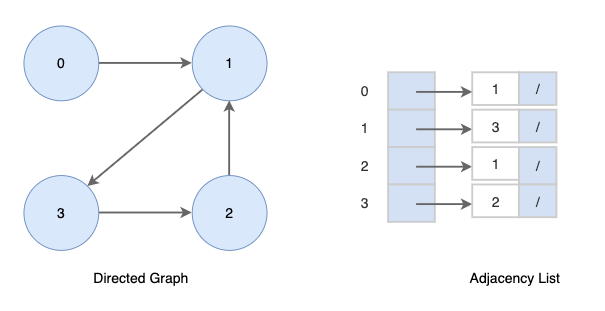
방향성 그래프를 인접리스트로 표현하면 다음과 같습니다.
인접 목록의 길이의 합은 그래프에 있는 간선의 수와 같습니다.
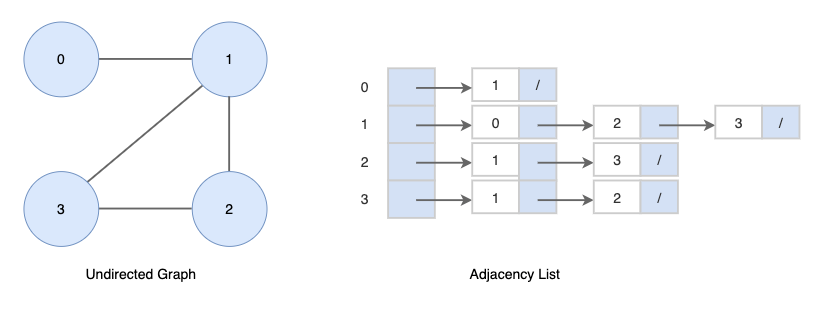
2. 무방향성 그래프 (Undirected Graph)
무방향성 그래프를 인접리스트로 표현하면 다음과 같습니다.
인접 목록의 길이의 합은 그래프에 있는 간선의 수의 두배와 같습니다.
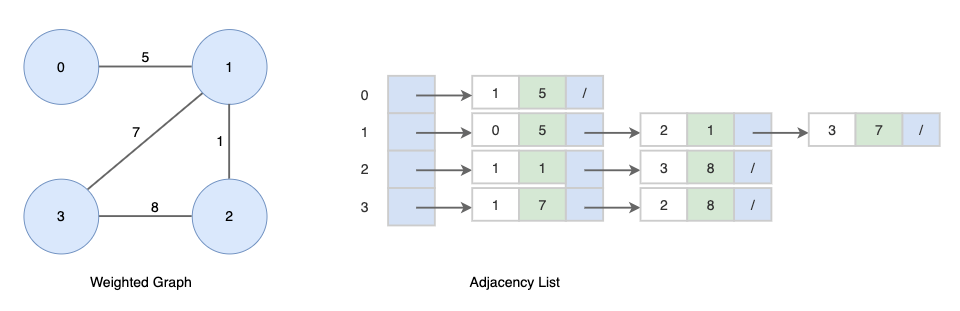
3. 가중치 그래프(Weighted Graph)
가중치 그래프에서는 가중치를 저장하기 위한 추가 필드가 필요합니다.
가중치 그래프를 인접리스트로 표현하면 다음과 같습니다.
구현
무방향 그래프를 생성하고 간선을 추가하는 코드입니다.
struct AdjListNode {
int dest;
struct AdjListNode* next;
};
typedef struct AdjListNode AdjListNode;
typedef struct AdjList {
AdjListNode* head;
} AdjList;
typedef struct Graph {
int vertexNumber;
AdjList* adj; // 인접한 정점을 저장하기 위한 공간
} Graph;
// n개의 정점을 가진 Grpah를 만든다간
Graph* createGraph(int n) {
int i = 0;
Graph *G = NULL;
G = (Graph*)malloc(sizeof(Graph));
G->vertexNumber = n;
G->adj = (AdjList*)malloc(sizeof(AdjList) * n);
for (i=0; i < n; i++) {
G->adj[i].head = NULL;
}
return G;
}
// 새로운 인접 리스트 노드를 생성한다.
AdjListNode* newAdjListNode (int w) {
AdjListNode* newNode = NULL;
newNode = (AdjListNode*)malloc(sizeof(AdjListNode));
newNode->dest = w;
newNode->next = NULL;
return newNode;
}
// 무방향그래프에 대한 새로운 간선을 추가한다.
void addEdge (Graph* g, int v, int w) {
AdjListNode* newNode=NULL;
newNode = newAdjListNode(w);
newNode->next = g->adj[v].head;
g->adj[v].head = newNode;
newNode = newAdjListNode(v);
newNode->next = g->adj[w].head;
g->adj[w].head = newNode;
}
// Graph를 출력한다.
void printGraph (Graph* g) {
int i = 0;
AdjListNode* temp = NULL;
for (i=0; i<g->vertexNumber; i++) {
temp = g->adj[i].head;
printf("V[%d] ", i);
while (temp) {
printf("-> %d ", temp->dest);
temp = temp->next;
}
printf("\n");
}
}
void main (void) {
Graph *g = NULL;
g= createGraph(4);
addEdge(g,0,1);
addEdge(g,1,2);
addEdge(g,1,3);
addEdge(g,2,3);
printGraph(g);
}Output:
V[0] -> 1
V[1] -> 3 -> 2 -> 0
V[2] -> 3 -> 1
V[3] -> 2 -> 1시간 복잡도 (Time Complexity) & 공간 복잡도 (Space Complexity)
시간 복잡도
- 어느 두 정점(i, j)에 부속된 간선이 있는지 체크하는 연산
- O(d) (d=degree(i))
- 정점 i에 있는 연결리스트를 순회하면서 j를 찾으면 되기 때문입니다.
- 임의의 한 정점(i)에 인접한 정점을 찾는 연산
- O(d) (d= degree(i))
- 정점 i에 있는 연결리스트를 순회하면 되기 때문입니다.
공간 복잡도
- O(|V|+|E|)
- 정점의 수만큼 공간이 필요하고 인접한 정점을 저장하기 위해 간선 수만큼의 추가 공간이 필요하기 때문입니다.




