그래프 (Graph) 알아보기
그래프(Graph)는 정점(Vertex)의 집합 V와 간선(Edge)의 집합 E로 구성된 비선형 데이터 구조입니다.
- 정점(Vertex) : 자료를 저장하려는 자료의 단위, 노드(Node)라고도 말함.
- 간선(Edge) : 정점 사이를 연결하는 선으로 두 정점 쌍 (u, v)로 표현함.
그래프(G)는 정점들의 집합 V와 간선들의 집합 E를 사용하여 (V, E)로 나타냅니다.
- G = (V , E)

V = {1, 2, 3, 4, 5}
E = {(1,2), (1,5), (2,3), (2,4), (2,5), (3,4), (4,5)}
그래프 용어
Directed edge & Undirected edge
- 방향성(유향) 간선 (Directed edge)
- 방향을 가진 정점의 쌍 (u, v)으로 화살표로 표현하고 단방향을 가리킵니다.
- 첫 번째 정점 u는 출발점을 의미하고 두 번째 정점 v는 도착점을 의미합니다.
- 방향성 간선을 가진 그래프를 방향성 그래프(Directed Graph)라고 합니다.
- 무방향성(무향) 간선 (Undirected edge)
- 방향이 없는 정점의 쌍 (u, v)으로 직선으로 표현한다.
- 무방향성 간선 (u, v)와 (v, u)는 같다. (양방향을 가리킴)
- 무방향성 간선을 가진 그래프를 무방향성 그래프(Undirected Graph)라고 합니다.

adjacent & incident
- 인접 (adjacent)
- 무방향성 그래프에서 정점 u, v에 대하여 간선(u, v)이 있으면 정점 u는 정점 v에 인접(adjacent) 하다고 한다. (역도 성립)
- 방향성 그래프에서 정점 u, v에 대하여 간선(u,v)이 있으면 정점 v는 정점 u에 인접한다고 한다. (역은 성립하지 않음.)
- 부속 (incident)
- 무방향 그래프에서 정점 u,v에 대하여 간선(u, v)이 있으면 간선(u, v)은 정점 u와 v에 부속(incident)한다고 합니다.

두 그래프 다 정점 2는 정점 1에 인접합니다.
하지만 방향 그래프에서 정점 1은 정점 2에 인접하지 않습니다. 왜냐하면 간선 (2,1)이 없기 때문입니다.
Self-loop & isolated
- self-loop
- 한 간선이 같은 정점에 부속해 있을 때 self-loop라고 합니다.
- e = (u, u)
- isolated
- 간선이 없는 경우를 말하며 간선이 없는 정점을 isolated vertex라고 합니다.

차수 (Degree)
- 차수(degree)는 정점에 연결된 간선의 수이고 정점 v의 차수는 d(v)로 표현합니다.
- 방향 그래프에서 차수는 진출 차수(out-degree)와 진입 차수(in-degree)의 합입니다.
- 진출 차수(out-degree): 정점을 나가는 간선의 수
- 진입 차수(in-degree): 정점으로 들어오는 간선의 수
- 무방향 그래프에서는 진입/진출 차수가 없으며 단순히 차수로 나타냅니다.
- self-loop인 경우 차수를 두 번 카운팅 합니다. 방향 그래프인 경우 진출/진입 차수가 각각 하나씩 카운팅 됩니다.

Undirected graph
- d(1)=3, d(2)=3, d(3)=2, d(4)=2
Directed graph
- d(1) = out-degree(=2) + in-degree(=1) = 3
- d(2) = out-degree(=1) + in-degree(=2) = 3
- d(3) = out-degree(=1) + in-degree(=1) = 2
- d(4) = out-degree(=1) + in-degree(=1) = 2
경로 (path)
- 정점 u에서 정점 v까지 도달하기 위한 인접한 정점들의 순서(sequence)입니다.
- 경로의 길이 (length of path)
- 경로 상에 있는 간선의 수입니다.
- 단순 경로 (simple path)
- 정점이 중복되지 않는 경로입니다.

경로 <0, 1, 3, 0, 2>의 길이는 4이고 단순 경로가 아닙니다.
경로 <0, 1, 2>의 길이는 2이고 중복되는 정점이 없기 때문에 단순 경로입니다.
순환 (cycle)
- 경로 중 시작 정점과 끝 정점이 같은 경우를 순환(cycle)이라고 합니다.
- 경로 <v0, v1, v2,..., vk>에서 v0=vk인 경우
- 단일 순환(simple cycle)
- 처음 정점과 끝 정점을 제외하고 정점이 중복되지 않는 순환을 단일 순환(simple cycle)이라고 합니다.
- 순환 <v0, v1, v2,..., vk>에서 v1, v2,..., vk가 서로 다른 경우

경로 <0, 1, 2, 3, 1, 0>는 순환(cycle)입니다.
경로 <0, 1, 3, 0>는 단순 순환(simple cycle)입니다.
연결(Connected) & 비연결(Disconnected)
- 두 정점을 포함하는 경로가 있다면 두 정점은 연결되었다(connected)고 하고 그렇지 않으면 비연결 되었다(disconnected)고 합니다.
- 방향 그래프에서 방향을 무시하고 보면 연결되어 있을 경우 연결되었다고 합니다.
- 방향성 그래프에서 임의의 노드 쌍 u, v에 대해 u에서 v 가는 경로, v에서 u로 가는 경로가 존재한다면, 해당 그래프는 강연 결(strongly connected)되었다고 말합니다.

그래프 G1은 어느 정점이든 경로가 존재하기 때문에 강연결입니다.
그래프 G2는 연결되었지만 정점 0에서 3으로 가는 경로가 없기 때문에 강연결은 아닙니다.
그래프 G3은 정점 0에서 2 로가는 경로가 없기 때문에 비연결입니다.
연결 요소 (connected components)
- 연결 요소란 서로 중복되지 않는 연결된 부분 그래프를 말합니다.
- 그래프가 연결돼있지 않다면 그래프는 연결 요소들의 집합으로 구성됩니다.
- 연결된 그래프는 하나의 연결 요소만 가지고 있습니다.
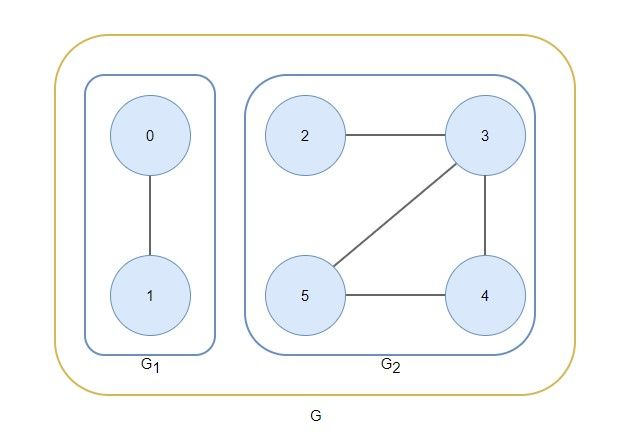
부분 그래프 G1, G2는 그래프 G의 연결 요소입니다.
그래프 유형
무방향성 그래프 (Undirected Graph)
- 무방향성 간선을 가진 그래프입니다.
- 무 방향 그래프는 모든 간선이 양방향입니다.
방향성 그래프 (Directed Graph, digraph)
- 방향성 간선을 가진 그래프입니다.
- 방향성 그래프는 모든 간선이 단방향입니다.
가중치 그래프 (Weighted Graph)
- 가중치 그래프는 각 간선에 가중치 또는 비용이 할당된 그래프입니다.

단순 그래프(Simple Graph)
- 단순 그래프는 중복된 간선과 loop가 없는 그래프입니다.
- 단순 그래프에서 정점의 개수가 n이라고 했을 때 최대 n-1개의 간선을 가질 수 있습니다.

완전 그래프 (Complete Graph)
- 완전 그래프는 간선의 수가 최대인 그래프입니다. 정점의 수가 n개이면 Kn으로 표현합니다.
- 정점 수 :n , 간선의 수: n*(n-1)/2

연결 그래프 (Connected Graph) & 비연결 그래프(Disconnected Graph)
- 모든 정점이 연결돼 있으면 연결 그래프이고 그렇지 않으면 비연결 그래프입니다.

그래프 G1은 연결 그래프입니다.
그래프 G2는 {0,1}, {2,3,4,5}가 연결되어 있지 않아 비연결 그래프입니다.
순환 그래프 (Cyclic Graph) & 비순환 그래프 (Acyclic Graph)
- 순환(cycle)을 가지고 있으면 순환 그래프이고 그렇지 않으면 비순환 그래프입니다.
- n개의 정점이 사이클을 이루고 있을 경우 Cn이라고 표시합니다.

희소 그래프 (Sparse Graph) & 밀집 그래프(Dense Graph)
- 희소 그래프는 노드수보다 간선 수가 적은 그래프를 말합니다. (보통 간선의 수가 |V|log|V|보다 적을 경우)
- 밀집 그래프는 노드수보다 간선 수가 큰 그래프입니다.

트리(Tree) & 포레스트(Forest)
트리 (Tree)
- 트리는 연결된 비순환 무방향성 그래프입니다. (Connected, Acyclic, Undirected Graph)
- 트리는 다음과 같은 특성이 있습니다.
- 간선의 수(|E|) = 정점의 수(|V|) - 1
- 두 정점은 단일 단순 경로 (unique simple path)로 연결됩니다.
- 트리에 간선을 하나 추가하면 순환(cycle)을 가집니다.
- 트리에 어떤 간선을 제거하면 트리는 더 이상 연결되지 않습니다. (disconnected)
포레스트 (Forest)
- 서로 중복되지 않는 트리들의 집합입니다. (트리를 분리한 집합)

사용 사례
- Social Networks
- Facebook, Linkedin ...
- City Road Network
- Networks rounting




