그래프 순회 (Graph traversal) 알아보기
그래프 순회(traversal)는 모든 정점을 방문하는 작업입니다.
그래프는 탐색하는 동안 동일 정점으로 다시 이동할 수 있는 싸이클이 있을 수 있습니다.
동일한 정점이 다시 처리되지 않도록 하려면 처리 후 정점을 방문(Visited)했다는 표시를 하여 중복 방문을 피하도록 합니다.
대표적으로 두 가지 방법이 있습니다.
- 깊이 우선 탐색 (DFS: Depth First Search)
- 너비 우선 탐색 (BFS: Breath First Search)
깊이 우선 탐색 (DFS: Depth First Search)
깊이 우선 탐색 (DFS: Depth First Search)은 그래프에서 최단 경로를 찾는 간선 기반 알고리즘입니다.
DFS는 형제 정점을 탐색하기 전에 자식 정점부터 탐색합니다.
트리의 전위순회와 유사하고 순서는 다음과 같습니다.
- 하나의 정점에서 시작합니다.
- 간선을 따라 다음 정점으로 방문합니다.
- 더 이상 탐색할 간선이 없으면 역추적(backtracking)을 통해 이전 정점으로 이동하면서 탐색하지 않은 간선이 있는지 확인합니다.
- 탐색 가능한 간선이 있다면 다시 간선을 따라 다음 정점으로 이동합니다.
- 모든 정점을 탐색할 때까지 3,4를 반복합니다.
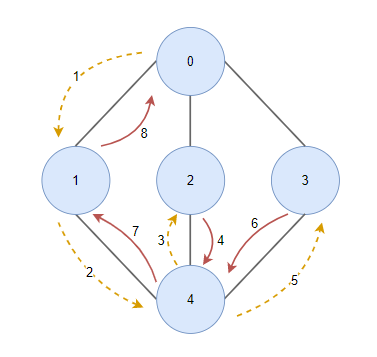
수행 과정
DFS는 역추적을 사용하는 재귀 알고리즘입니다. 이 재귀의 특성은 스택 자료구조를 사용하여 구현할 수 있습니다.
수행 과정은 다음과 같습니다.
- 시작 정점을 스택에 push합니다.
- 스택에 맨 위에 있는 정점을 pop 하고 방문 표시를 합니다.
- pop 된 정점에서 방문하지 않은 인접한 정점들을 스택에 push 합니다.
- 스택이 빌 때까지 2번 3번을 반복합니다.
예시)
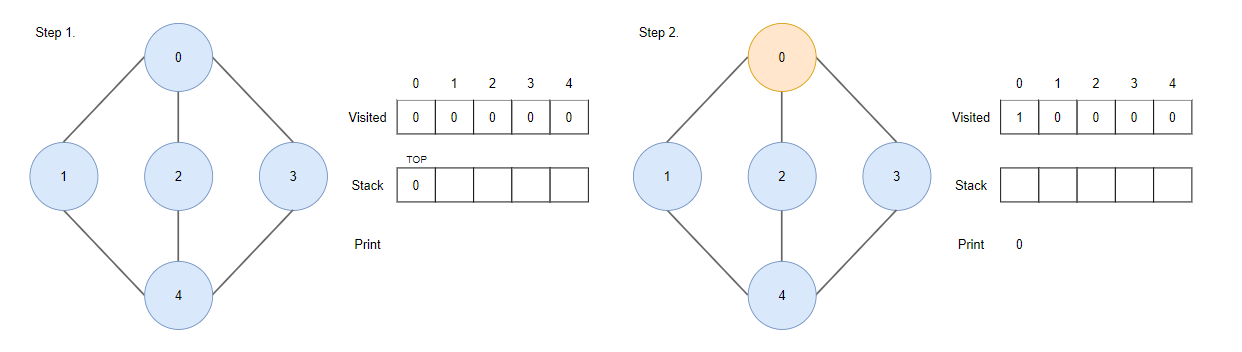
Step 1.
- 시작 정점 0을 스택에 push 합니다.
Step2.
- 스택에 맨 위에 있는 정점 0을 pop 하고 방문 표시를 합니다.
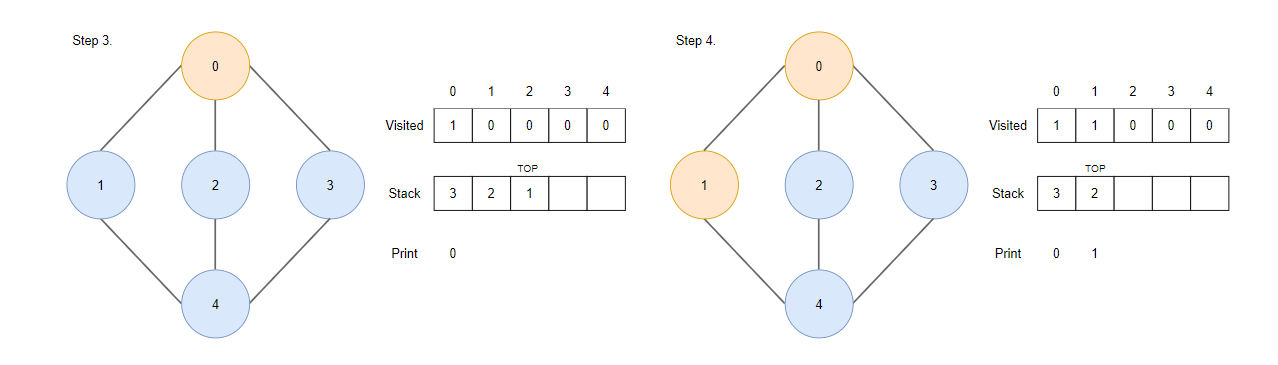
Step3.
- pop 된 정점 0에서 방문하지 않은 인접한 정점 1,2,3을 스택에 push 합니다. (3, 2, 1 순으로 스택에 저장된다고 가정합니다.)
Step4.
- 스택에 맨 위에 있는 정점 1을 pop 하고 방문 표시합니다.
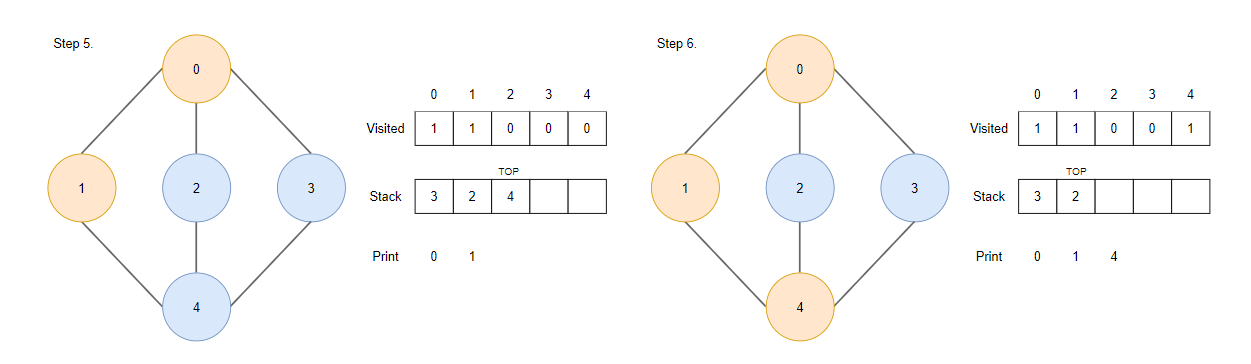
Step5.
- pop 된 정점 1에서 방문하지 않은 인접한 정점 4를 스택에 push 합니다.
Step6.
- 스택 맨 위에 있는 정점 4를 pop 하고 방문 표시합니다.
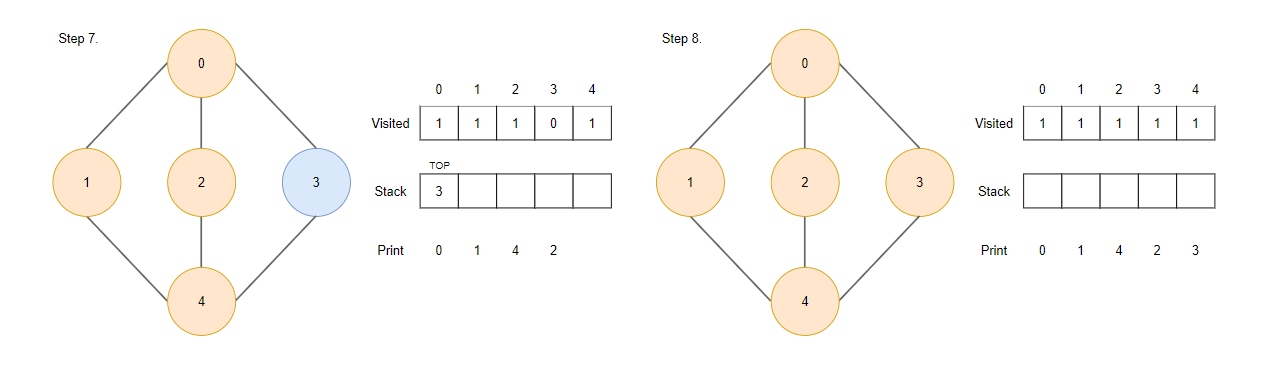
Step7.
- pop 된 정점 4에서 방문하지 않은 인접한 정점이 더 이상 없기 때문에 스택 맨 위에 있는 정점 2를 pop하고 방문 표시합니다.
Step8.
- pop된 정점 2에서 방문하지 않은 인접한 정점이 더이상 없기 때문에 스택 맨 위에 있는 정점 3을 pop하고 방문 표시합니다. 스택에 정점이 더이상 없기 때문에 탐색을 종료합니다.
구현
그래프는 인접 리스트를 사용합니다. (이전 글 그래프 표현 및 구현 참고)
visited [] 배열은 0으로 초기화된 전역 변수입니다.
visited 값이 1이면 방문했다는 의미입니다.
재귀를 사용한 구현
재귀를 사용하면 쉽게 DFS를 구현할 수 있습니다.
void DFS (struct Graph *G, int s) {
AdjListNode *temp = NULL;
visited[s] = 1;
printf("%d\n", s);
// 재귀를 통해 방문하지 않은 인접 정점으로 이동합니다.
for (temp = G->adj[s].head; temp != NULL; temp= temp->next) {
v = temp->dest;
if(visited[v] == 0) {
DFS(G, v);
}
}
}스택을 사용한 구현
스택을 사용하여 비재귀로 구현할 수도 있습니다.
void DFS (struct Graph *G, int s) {
AdjListNode *temp = NULL;
Stack *S = createStack();
// 시작 정점을 스택에 push 합니다.
push(S, s);
while (!isEmpty(S)) {
// 스택에 있는 정점을 pop하고 방문 표시를 합니다.
s = pop(S);
if (visited[s] == 0) {
visitied[s] = 1;
printf("%d\n", s);
}
// 방문하지 않은 인접 정점을 스택에 push합니다.
for (temp = G->adj[s].head; temp != NULL; temp=temp->next) {
v = temp->dest;
if (visitied[v] == 0) {
push(S, v);
}
}
}
}시간 복잡도 (Time Complexity)
V는 정점의 수이고 E는 간선의 수입니다.
- 인접 리스트를 사용할 때 \( O(V+E) \)
- 인접 행렬을 사용할 때 \( O(V^2) \)
DFS의 응용
- 위상 정렬 (Topological sorting)
- 연결 컴포넌트 (connected components) 찾기
- 강한 연결 컴포넌트 (stringly connected components) 찾기
- 미로 문제 (Maze problems) 등등
너비 우선 탐색 (BFS: Breath First Search)
너비 우선 탐색 (BFS: Breath First Search)은 그래프에서 최단 경로를 찾는 정점 기반 알고리즘입니다.
BFS는 자식 정점을 방문하기 전에 형제 정점을 방문합니다.
BFS는 레벨 순으로 운행하는데 순서는 다음과 같습니다.
- 처음에 레벨 0에 있는 한 정점에서 시작합니다.
- 먼저 레벨 1의 모든 정점들을 방문합니다. (시작 정점에서 거리가 1인 정점들)
- 그다음 레벨 2의 모든 정점들을 방문합니다. (시작 정점에서 거리가 2인 정점들)
- 이런 식으로 레벨을 늘리면서 모든 레벨에 있는 노드들을 방문할 때까지 반복합니다.
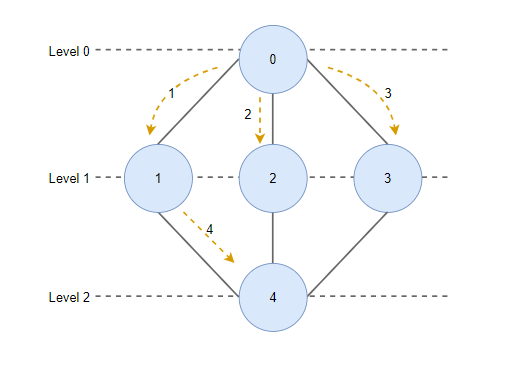
수행 과정
BFS는 큐 자료구조를 사용하며, 큐는 한 레벨의 정점들을 저장하는 데 사용됩니다.
초기에 모든 정점들은 방문하지 않은 상태에서 시작하고 큐에서 삽입된 정점들은 방문한 것으로 표시합니다.
큐에서 제거된 정점에서 인접한 정점들 중 방문한 적이 없는 정점들을 큐에 삽입합니다.
수행 과정은 다음과 같습니다.
- 모든 정점을 방문하지 않는 상태로 표시합니다.
- 시작 정점을 방문하여 방문 표시를 한 뒤 큐에 삽입합니다.
- 큐에서 첫 번째 정점을 제거하고 제거된 정점에서 방문하지 않은 인접한 정점을 방문하여 방문 표시를 한 뒤 큐에 삽입합니다.
- 인접한 정점이 없는 경우 큐에서 첫 번째 정점을 빼옵니다.
- 큐가 빌 때까지 3번 4번을 반복합니다.
예시)
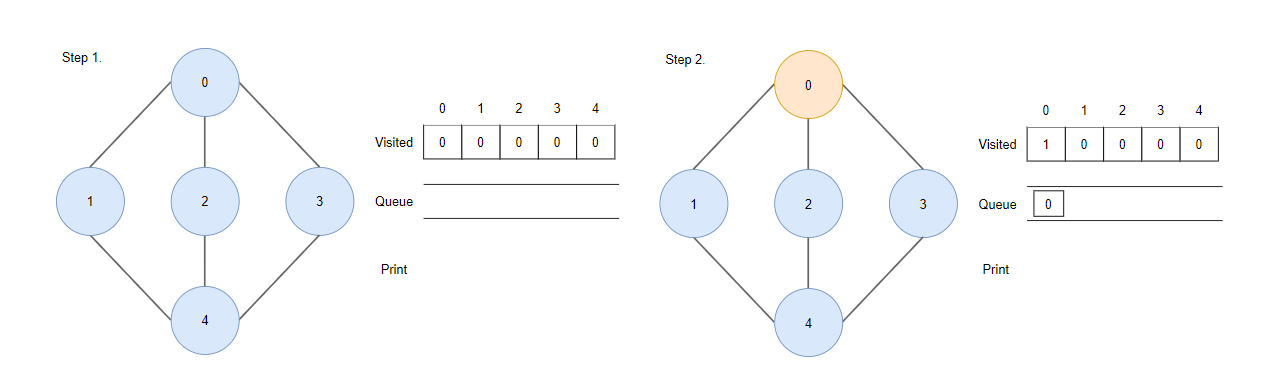
Step1.
- 모든 정점을 방문하지 않는 상태로 표시합니다.
Step2.
- 시작 정점(0)을 방문하여 방문 표시를 한 뒤 큐에 삽입합니다.
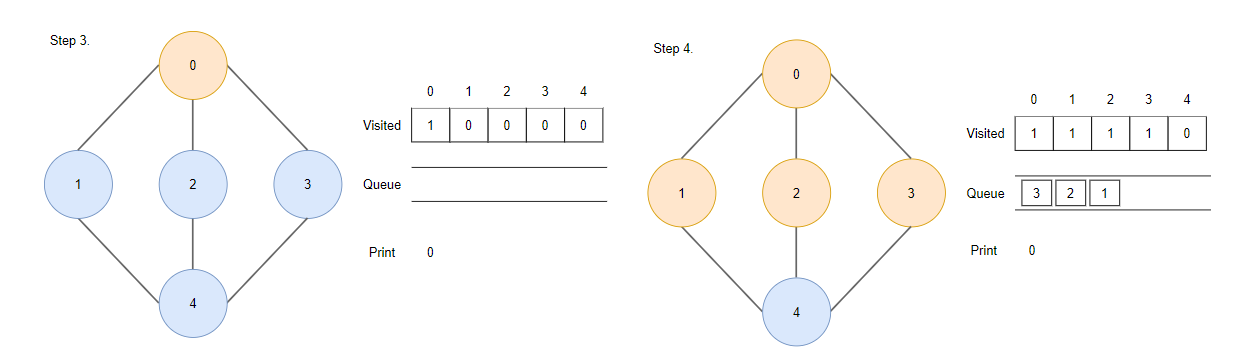
Step3.
- 큐에서 첫 번째 정점(0)을 제거합니다.
Step4.
- 정점 0에서 인접한 정점들 중 방문한 적이 없는 정점 1,2,3을 방문하여 방문 표시를 한 뒤 큐에 삽입합니다.
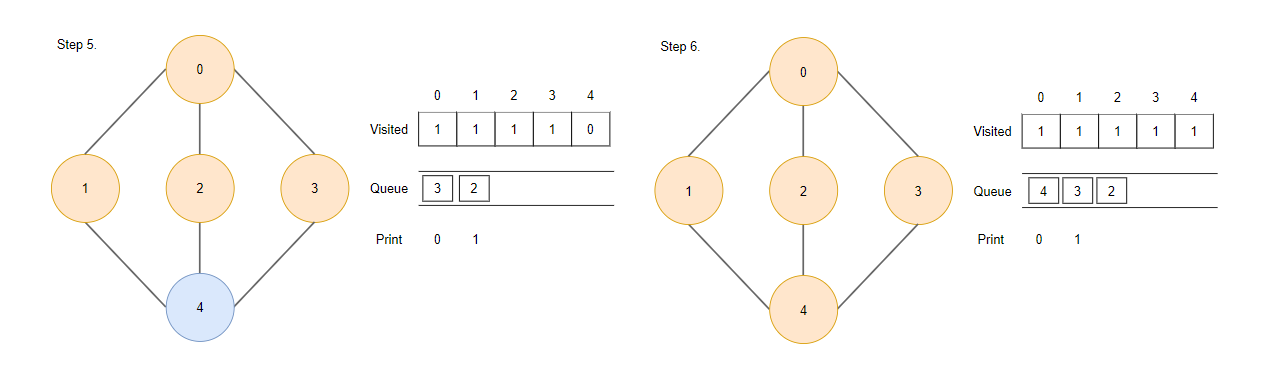
Step5.
- 큐에서 첫 번째 정점(1)을 제거합니다.
Step6.
- 정점 1에서 인접한 정점들 중 방문한 적이 없는 정점 4를 방문하여 방문 표시를 한 뒤 큐에 삽입합니다.
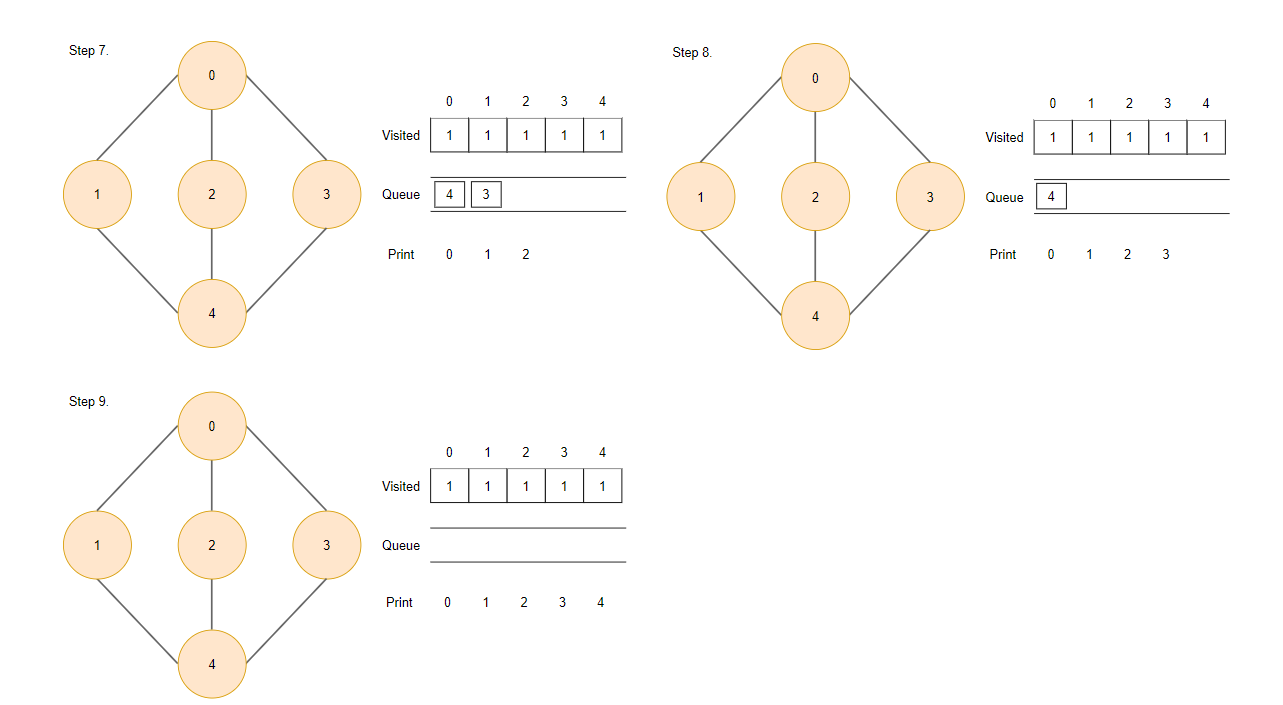
Step7~9.
- 모든 정점을 방문하였기 때문에 큐에서 정점들을 하나씩 제거합니다.
구현
그래프는 인접 리스트를 사용합니다.
visited [] 배열은 0으로 초기화된 전역 변수입니다.
visited 값이 1이면 방문했다는 의미입니다.
void BFS (struct Graph *G, int s) {
int i = 0;
struct Queue *Q = CreateQueue();
// 시작 정점을 방문하여 방문표시를 한뒤 큐에 삽입.
visited[s] = 1;
EnQueue(Q, s);
while(!IsEmptyQueue(Q)) {
// 큐에 첫번째 정점을 제거하여 가져옴
s = DeQueue(Q);
printf("%s ", s);
// 방문하지 않은 인접한 정점들을 찾아 방문 표시를 하고 큐에 삽입
for (temp = Q->adj[s].head; temp != NULL; temp = temp->next) {
int v = temp->dest;
if(visited[v] == 0) {
visited[v] = 1;
EnQueue(Q, v);
}
}
}
printf("\n");
}시간 복잡도 (Time Complexity)
V는 정점의 수이고 E는 간선의 수입니다.
- 인접 리스트를 사용할 때 \( O(V+E) \)
- 인접 행렬을 사용할 때 \( O(V^2) \)
BFS의 응용
- shortest path in undirected graph
- cycle detection
- bipartite check
- MST(mininum spaning tree) in unweighted graph
- Network Broadcasting
- 연결 컴포넌트(Connected components) 찾기 등등




