벨만-포드 알고리즘(Bellman-Ford Algorithm) 알아보기
벨만-포드 알고리즘 (Bellman-Ford Algorithm)은 최단 경로(Shortest path) 문제 중에 Single-source path 찾는 알고리즘입니다.
최단 경로 문제는 아래 글을 참고하시기 바랍니다.
https://yoongrammer.tistory.com/87
최단 경로(Shortest path) 문제 개념
목차 최단 경로(Shortest path) 문제 알아보기 최단 경로 문제(shortest-paths proble)란 두 노드를 잇는 가장 짧은 경로를 찾는 문제입니다. 여기서 가장 짧은 경로란 간선의 가중치 합이 가장 작은 경로
yoongrammer.tistory.com
특징
- brute force strategy를 사용합니다.
- 동일 문제에 대해 다익스트라의 알고리즘보다 느리지만 음수 간선을 가진 그래프에서도 사용 가능합니다.
- 그래프에 음의 가중치 사이클 여부를 확인할 수 있습니다.
음의 가중치 사이클이 없으면 true를 반환하고 그렇지 않으면 false를 반환합니다.
구현
다익스트라 알고리즘과 마찬가지로 Relax 연산을 사용합니다.
다익스트라 알고리즘은 greedy 한 방식으로 최단경로를 찾기 위해 우선순위 큐를 사용하는 반면 벨만-포드 알고리즘은 단순히 모든 간선에 대해 Relax를 수행합니다.
의사 코드는 다음과 같습니다.
BELLMAN-FORD(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 for i 1 to |V[G]| - 1
3 do for each edge (u, v) ∈ E[G]
4 do RELAX(u, v, w)
5 for each edge (u, v) ∈ E[G]
6 do if d[v] > d[u] + w(u, v)
7 then return FALSE
8 return TRUE- 그래프에 있는 모든 정점을 초기화 합니다.
- 모든 정점은 d[v] = ∞, π[v] = nil 로 초기화되고 그중 시작 정점인 s는 0으로 초기화합니다.
- 2~4 라인은 모든 간선에 대한 Relax연산을 "정점 수 - 1"회 반복합니다.
- 5~8 라인은 음의 가중치 사이클이 있는지 검사하고 있다면 false를 반환하고 없으면 true를 반환합니다.
INITIALIZE-SINGLE-SOURCE, Relax 연산에 대해서는 위 링크에 있는 최단경로 문제 개념을 참고하시기 바랍니다.
그림 예시
다음은 벨만-포드 알고리즘의 그림 예시입니다.
- 소스는 정점 z입니다. d 값은 꼭짓점 내에 표시되고 주황색 간선은 π 값을 나타냅니다.
- d : 시작 정점부터 현재 정점까지의 최단경로 측정치(shortest path estimate)
- π : 시작 정점부터 현재 정점까지의 최단경로상에서 현재 정점의 직전 정점(predecessor)
- 간선의 relax연산은 사전 순으로 수행한다고 가정합니다. (순서는 구현에 따라 다름)
- 순서 : (u, v),(u, x), (u, y), (v, u), (x, v), (x, y), (y, v), (y, z), (z, u), (z, x)
- 초기화 작업을 합니다.
- 각 정점 v ∈ V에 대해서 s가 시작 정점이라고 했을 때, d[s] = 0, d[v] = ∞, π[v] = NIL로 초기화합니다.

- 각 정점 v ∈ V에 대해서 s가 시작 정점이라고 했을 때, d[s] = 0, d[v] = ∞, π[v] = NIL로 초기화합니다.
- 정점의 수 - 1 회만큼 모든 간선에 대한 relax연산을 사전 순으로 수행합니다. 이 그림에선 총 4(5-1) 회 반복합니다.
- 모든 간선의 relax연산을 사전 순으로 수행합니다.

- 모든 간선의 relax연산을 사전 순으로 수행합니다.

- 모든 간선의 relax연산을 사전 순으로 수행합니다.
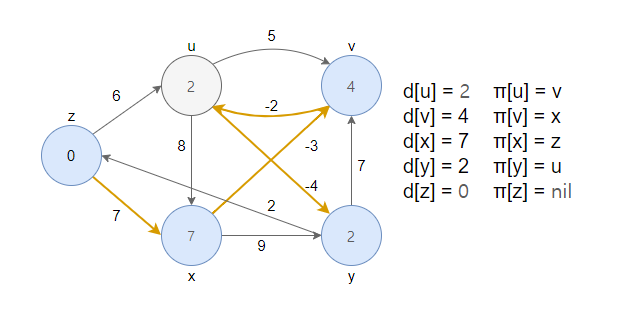
- 모든 간선의 relax연산을 사전 순으로 수행합니다. 이 값이 최종 d, π값이 됩니다.

- 모든 간선의 relax연산을 사전 순으로 수행합니다.
이 그림에선 음의 가중치 사이클을 가지고 있지 않으므로 true를 반환합니다.
성능
벨만-포드 알고리즘의 성능은 다음과 같습니다.
V는 정점의 수이고 E는 간선의 수입니다.
초기화 작업 (line 1)
- \(O(V)\)
RELAX 연산 (line 2 ~ 4)
- RELAX 연산의 시간 복잡도는 \(O(1)\)이고 총 E회 수행하기 때문에 매 차례마다 \(O(E)\)의 시간이 소요되고 총 \(V-1\) 회의 차례를 수행하게 됩니다. 그러므로 총 \(O((V-1) E)= O(VE)\)의 시간이 걸립니다.
음의 가중치 사이클 검사 (line 5 ~ 7)
- \(O(E)\)
그러므로 벨만-포드 알고리즘의 시간 복잡도는 \(O(V+VE+E) = O(VE)\)입니다.




