최단 경로(Shortest path) 문제 알아보기
최단 경로 문제(shortest-paths proble)란 두 노드를 잇는 가장 짧은 경로를 찾는 문제입니다.
여기서 가장 짧은 경로란 간선의 가중치 합이 가장 작은 경로를 말합니다.
경로 p = <v0, v1,... vk>의 가중치(w) 합이 다음과 같다면
$$ w(p) = \sum_{i=1}^k w(v_{i-1},v_{i}) $$
정점 u에서 v까지의 최단경로 값은 다음과 같이 표시합니다.
$$ \delta(u,v) = \begin{cases} min\{w(p) : u \overset{p}\rightsquigarrow v \}, & \mbox{if u에서 v로 가는 경로가 있다면} \\ \infty, & \mbox{if u에서 v로 가는 경로가 없다면} \end{cases}$$
가중치가 없는 그래프에서 최단경로를 찾을 경우 가중치가 1인 최단 경로를 찾는 것과 같습니다.
이것은 간선이 가장 적은 경로를 찾는 것과 같습니다.
표현
다음 그림은 정점 s에서 출발하는 최단 경로를 나타낸 것입니다.
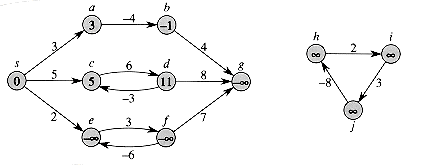
각 정점에 표시된 값은 s에서 출발한 최단 경로 값(δ)입니다.
- 정점 s는 시작 정점이기 때문에 0으로 표시합니다.
- 정점 s에서 a로 가는 경로는 하나이기 때문에 δ(s, a) = w(s, a) = 3입니다.
- 정점 s에서 b로 가는 경로 또한 하나이기 때문에 δ(s, b) = w(s, a) + w(a, b) = 3 + (-4) = -1입니다.
- 정점 s에서 c로 가는 경로에는 사이클 <c, d, c>가 있어 무수히 많지만(<s, c>, <s, c, d, c>, <s, c, d, c, d, c>...) 사이클 <c, d, c>는 양수 가중치(6 + (-3) = 3)를 가지기 때문에 하나의 최단 경로 δ(s, c) = 5 만 갖습니다.
- 비슷한 이유로 정점 s에서 d로 가는 최단 경로 값은 δ(s, d) = w(s, c) + w(c, d) = 11입니다.
- 정점 s에서 e 또는 f로가는 경로에는 사이클 <e, f, e>가 있고 이 사이클은 음수 가중치(3 + (-6) = -3)를 가지기 때문에 사이클을 반복해서 순회한다면 -∞로 감소하기 때문에 δ(s, e) = δ(s, f) = -∞ 로 표시합니다.
- 정점 s에서 g까지의 경로는 정점 f를 통해서 접근할 수 있기 때문에 δ(s, g) = -∞입니다.
- 정점 h, i, j는 음수 가중치를 갖는 사이클이지만 정점 s에서 접근할 수 있는 경로가 없기 때문에 ∞로 표시합니다.
최단 경로 문제 유형
최단 경로 문제에는 다음과 같은 유형들이 있습니다.
- Single-source (one to all)
- 단일 정점 v에서 출발하여 모든 다른 정점으로 도착하는 최단 경로를 찾는 문제
- Single-destination (all to one)
- 모든 정점에서 출발하여 단일 정점 v로 도착하는 최단 경로를 찾는 문제
- 그래프 내의 간선을 거꾸로 뒤집으면 single-source 문제와 동일
- Single-pair (one to one)
- 단일 정점 s에서 출발하여 단일 정점 v로 도착하는 최단 경로를 찾는 문제
- 이 문제는 signle-source로 해결할 수 있고 최악의 경우 single-source 보다 빠른 알고리즘은 없음
- All-pairs (all to all)
- 모든 정점 쌍에 대해서 최단 경로를 찾는 문제
- 각 정점에서 single-source 알고리즘을 한 번씩 실행하여 해결할 수 있지만 더 빠른 방법이 존재함
모든 최단경로 알고리즘 유형은 single-source를 응용하면 해결이 가능합니다.
최단 경로의 기본 특성
1. 최단 경로의 부분 경로 또한 최단 경로이다.
- 다음 그림처럼 경로 \(P_{uv}\)를 최단 경로라고 한다면 부분 경로 \(P_{xy}\) 또한 최단 경로입니다.

- \( δ( u , v ) = w ( P ) = w ( P_{ux} ) + w ( P_{xy} ) + w ( P_{yv} ) \)
- \(P_{xy}\)보다 짧은 \(P'_{xy}\)가 있다면 \(P_{uv}\)가 최단 경로라는 사실은 모순이 됩니다.
- 이 속성은 Optimal substructure 구조를 가지고 있어 탐욕 알고리즘(greedy algorithms)과 동적 프로그래밍(dynamic programming)을 적용할 수 있습니다.
2. 최단 경로는 사이클을 포함하지 않는다.
- 음수 사이클을 포함하는 경우 사이클을 순회할수록 가중치가 계속 줄어들기 때문에 최단 경로를 찾을 수 없습니다.
- 양의 사이클을 포함하는 경우 사이클을 빼면 더 짧은 경로를 얻을 수 있습니다.
3. 최단 경로는 하나 이상일 수 있다.
- 다음 그림처럼 최단 경로는 여러 개일 수 있습니다.

- \(δ(s , x) = w(P_{st}) + w(P_{tx})\) or \(w(P_{st}) + w(P_{ty}) + w(P_{yx})\)
- \(δ(s , z) = w(P_{sy}) + w(P_{yz})\) or \(w(P_{st}) + w(P_{ty}) + w(P_{yx}) + w(P_{xz})\)
알고리즘(Algorithm)
모든 최단 경로 알고리즘에는 다음과 같은 공통점이 있습니다.
출력 (Output)
모든 최단 경로 알고리즘은 다음과 같은 출력 값을 가지고 있습니다.
d[v]
- s 정점에서 시작하여 v정점까지의 최단 경로 가중치의 상한으로 최단경로 측정치(shortest path estimate)
- 알고리즘 초반에 d[s] = 0, d[v]=∞ 로 초기화합니다.
- 알고리즘을 진행되면서 d[v]의 값이 감소할 수 있지만 항상 d[v] ≥ δ(s, v)를 유지합니다.
- 최종적으로 d[v] = δ(s, v)가 됩니다.
π[v]
- 정점 s에서 v까지의 최단경로상에서 v의 직전 정점(predecessor)
- 알고리즘 초반에 π[v] = null로 초기화합니다.
- 알고리즘 종료 후 π[v] 값이 null이 아니라면 π[v] 은 정점 s가 루트인 최단 경로 트리(shortest path tree)가 됩니다.
- π[v] 값을 사용하여 최단경로를 출력할 수 있습니다.
연산 (Operation)
모든 최단 경로 알고리즘은 다음과 같은 연산이 있습니다.
초기화 (Initialization)
- d[v], π[v] 값을 초기화하는 연산입니다.
의사 코드는 다음과 같습니다.
INITIALIZE-SINGLE-SOURCE(G,s)
for each vertex v ∈ V[G]
do d[v] <- ∞
π[v] <- NIL
d[s] <- 0각 정점 v ∈ V에 대해서 s가 시작 정점이라고 했을 때, d[s] = 0, d[v] = ∞, π[v] = NIL로 초기화합니다.
이완 (Relaxation)
탐색 도중 더 짧은 경로를 발견하게 되면 d[v]와 π[v] 값을 갱신해주는 연산입니다.
알고리즘을 수행하는 과정에서 경로를 줄여나간다는 의미로 이완 (relaxation)이라는 이름을 사용합니다.
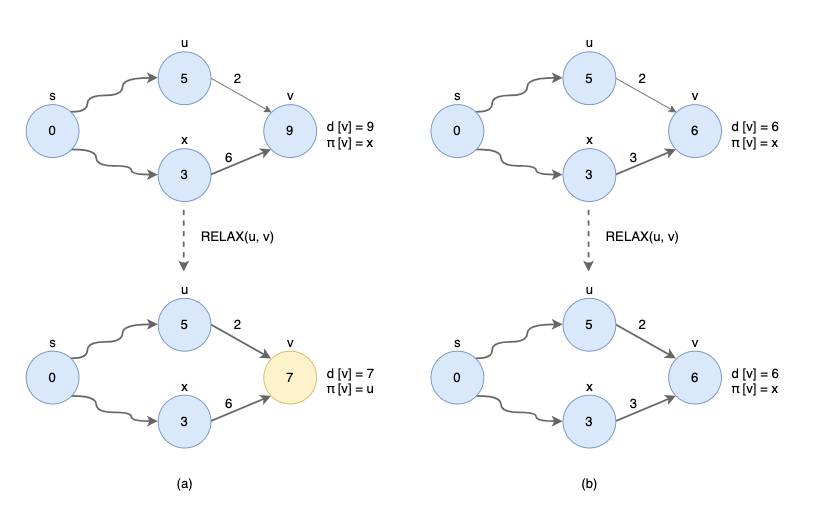
위 그림은 relaxation 과정입니다. 각 정점의 값은 d[v] 값입니다.
- (a) 그림은 이완 전 d[v] > d[u] + w(u,v)이기 때문에 d[v]값이 감소되고 π[v] 값은 u로 변경됩니다.
- (b) 그림은 이완 전 d[v] ≤ d[u] + w(u,v)이기 때문에 d[v], π[v] 값이 변경되지 않습니다.
의사 코드는 다음과 같습니다.
RELAX(u, v, w)
if d[v] > d[u] + w(u,v)
then d[v] <- d[u] + w(u,v)
π[v] <- ud[v] > d[u] + w(u,v)인 경우 d[v], π[v] 값을 변경해 줍니다.
최단경로 알고리즘은 초기화(Initialization) 연산을 한번 호출 한 다음 반복적으로 이완(relaxation)을 호출합니다.
알고리즘마다 이완(relaxation)을 호출하는 횟수와 순서가 다릅니다.
대표적으로 다익스트라(Dijkstra)와 벨만 포드(Bellman-Ford) 알고리즘이 있으며, all-pairs 최단경로 문제는 플로이드 와셜 (Floyd-Warshall) 알고리즘이 널리 쓰입니다.




