위상 정렬(Topological sort) 개념 및 구현
비순환 방향 그래프 (DAG: Directed Acyclic Graph)
Directed Acyclic Graph (DAG)는 사이클이 없는 방향 그래프입니다.
DAG는 이벤트 간의 우선순위를 나타내기 위해 주로 사용됩니다.

위상 정렬(Topological sort)
위상 정렬(Topological sort)은 비순환 방향 그래프(DAG)에서 정점을 선형으로 정렬하는 것입니다.
모든 간선 (u, v)에 대해 정점 u가 정점 v보다 먼저 오는 순서로 정렬이 됩니다.
그래프가 DAG가 아닌 경우 그래프에 대한 위상 정렬은 불가능합니다.
그래프에 사이클이 있으면서 두 정점 u,v가 사이클 속에 위치한 정점일 경우, 정점 u가 v보다 먼저 오거나 v가 u보다 먼저 올 수 있기 때문입니다.
위상 정렬 활용예로 대학교 선수과목을 들 수 있습니다.
특정 수강과목에 선수과목이 있다면 그 선수과목부터 수강해야 합니다. 여기서 위상 정렬은 특정 수강과목을 위해 필요한 선수과목의 정렬입니다.
위상 정렬된 정점을 수평선으로 나타내면 다음과 같습니다.

위상 정렬 결과 하나의 DAG에서 하나 이상의 위상 순서(Topological order)가 나올 수 있으며 모든 간선은 오른쪽만 가리키게 됩니다.
구현
구현 방법에는 in_degree를 사용하는 BFS(Breath First Search) 방법과 DFS(Depth First Search)를 사용하는 방법이 있습니다.
정점의 위상 순서를 저장할 리스트 T를 사용하고, 정점 방문 여부를 저장하기 위해 visited [N] 배열을 사용합니다.
In-degree 방법 (BFS 방법)
정점에 들어오는 간선수를 저장하기 위해 in_degree[N] 배열을 사용합니다. 여기서 i번째 요소는 정점 i로 들어오는 가장자리 수를 저장합니다.
동작 방식은 다음과 같습니다.
- 모든 정점의 in_degree를 설정합니다.
- in_degree가 0인 정점은 방문한 것으로 표시하고 큐에 정점을 추가합니다.
- 큐가 빌 때까지 순회하며 다음 작업을 수행합니다.
3.1. 큐의 앞 요소를 dequeue()로 가져와 T[]에 append합니다.
3.2. dequeue()한 정점에 인접한 정점중 방문하지 않은 정점의 in_degree를 하나 감소시킵니다.
3.3. in_degree 감소 후 값이 0이면 해당 정점은 queue에 enqueue() 하고 방문한 것으로 표시합니다.
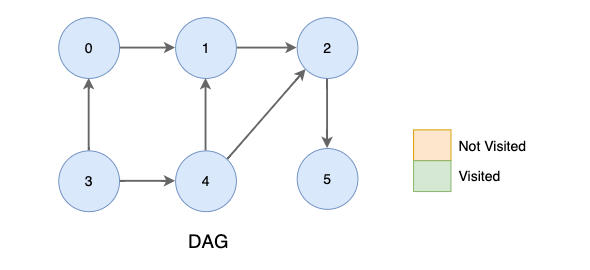
Step 1.
- 모든 정점의in_degree를 설정합니다.

Step 2.
- in_degree가 0인 정점 3을 큐에 삽입하고 방문표시합니다.

Step 3.
- 큐에서 정점 3을 dequeue()로 가져와 T[]에 append 합니다.
- 정점 3에 인접한 정점중 방문하지 않은 정점 (0, 4)의 in_degree를 하나 감소합니다.
- in_degree 값이 0인 정점 0, 4를 queue에 enqueue() 하고 방문표시합니다.

Step 4.
- 큐에서 정점 0을 dequeue()로 가져와 T[]에 append 합니다.
- 정점 0에 인접한 정점중 방문하지 않은 정점 1의 in_degree를 하나 감소합니다.

Step 5.
- 큐에서 정점 4를 dequeue()로 가져와 T[]에 append 합니다.
- 정점 4에 인접한 정점중 방문하지 않은 정점 (1,2)의 in_degree를 하나 감소합니다.
- in_degree값이 0인 정점 1을 queue에 enqueue()하고 방문표시합니다.

Step 6.
- 큐에서 정점 1을 dequeue()로 가져와 T[]에 append합니다.
- 정점 1에 인접한 정점중 방문하지 않은 정점 2의 in_degree를 하나 감소합니다.
- in_degree값이 0인 정점 2를 queue에 enqueue() 하고 방문표시합니다.

Step 7.
- 큐에서 정점 2를 dequeue()로 가져와 T[]에 append 합니다.
- 정점 2에 인접한 정점중 방문하지 않은 정점 5의 in_degree를 하나 감소합니다.
- in_degree값이 0인 정점 5를 queue에 enqueue()하고 방문표시합니다.

Step 8.
- 큐에서 정점 5를 dequeue()로 가져와 T[]에 append 합니다.
- 더 이상 queue에 정점이 없기 때문에 종료합니다.

구현
- 그래프는 인접 리스트를 사용합니다.
- in_degree[], visitied[] 배열은 0으로 초기화된 전역 변수입니다.
- append() 함수는 정점을 리스트 뒤에 추가하는 함수입니다. 추가 후 노드 T는 리스트의 head를 가리킵니다.
void TopologicalSort (Graph *G)
{
int i = 0;
AdjListNode *temp = NULL;
struct Node *T = NULL;
struct Queue *Q = createQueue(G->vertexNumber);
// 정점으로 들어오는 간선수(in_degree)를 설정한다.
for (i = 0; i < G->vertexNumber; i++) {
for (temp = G->adj[i].head; temp != NULL; temp=temp->next) {
in_degree[temp->dest]++;
}
}
// in_degree가 0인 정점은 방문한 것으로 표시하고 큐에 삽입
for (i = 0; i < G->vertexNumber; i++) {
if(in_degree[i] == 0) {
visitied[i]=1;
enqueue(Q, i);
}
}
// 큐가 빌때까지 순회한다.
while (!isEmpty(Q)) {
// 큐에 있는 정점을 하나 빼오고 T에 append한다.
int vertex = dequeue(Q);
append(&T, vertex);
// 인접 정점을 순회하며 방문하지 않은 정점에 in_degree를 하나 감소시킨다.
for (temp = G->adj[vertex].head; temp != NULL; temp=temp->next) {
if (visitied[temp->dest] == 0 && --in_degree[temp->dest] == 0) {
enqueue(Q, temp->dest);
visitied[temp->dest] = 1;
}
}
}
// 위상 정렬된 위상 순서를 출력한다.
printList(T);
}시간 복잡도 (Time Complexity)
V는 정점의 수이고 E는 간선의 수입니다.
- 인접 리스트를 사용할 때 \(O(V+E)\)
- 인접 행렬을 사용할 때 \(O(V^2)\)
DFS 방법
DFS는 in_degree가 필요 없고 재귀를 사용합니다.
그래프의 DFS와 방식은 같습니다.
- 모든 정점을 순회하며 방문하지 않은 정점에 대해서 DFS를 수행합니다.
- DFS 수행방식은 다음과 같습니다.
2.1. 하나의 정점에서 시작합니다.
2.2. 방문표시를 하면서 간선을 따라 다음 정점으로 방문합니다.
2.3. 더 이상 방문할 간선이 없으면 리스트 앞에 정점을 추가하고
역추적(backtracking)을 통해 이전 정점으로 이동하면서 방문하지 않은 간선이 있는지 확인합니다.
2.4.방문 가능한 간선이 있다면 다시 간선을 따라 다음 정점으로 이동합니다.
2.5. 모든 정점을 탐색할 때까지 2.2~2.4를 반복합니다.


구현
- 그래프는 인접리스트를 사용합니다.
- visitied[] 배열은 0으로 초기화된 전역 변수입니다.
- LIFO(Last In First Out) 순으로 정점을 관리하기 위해 리스트대신 스택을 사용합니다.
void topologicalSort_DFS (Graph *G) {
int i = 0;
AdjListNode *temp = NULL;
Stack *S = createStack(G->vertexNumber);
// 모든 정점을 순회하며 방문하지 않은 정점에 대해서 DFS를 수행
for (i = 0; i < G->vertexNumber; i++) {
if (!visitied[i]) {
DFS(G,i,S);
}
}
// 위상 정렬된 위상 순서를 출력한다.
printStack(S);
}
void DFS (Graph *G, int v, Stack *S)
{
AdjListNode *temp = NULL;
visitied[v] = 1;
// 재귀를 통해 방문하지 않은 인접 정점으로 이동한다.
for (temp = G->adj[v].head; temp != NULL; temp=temp->next) {
if (!visitied[temp->dest])
DFS(G,temp->dest,S);
}
// 더이상 방문할 간선이 없다면 리스트 앞에 정점을 추가한다.
push(S, v);
}시간 복잡도 (Time Complexity)
V는 정점의 수이고 E는 간선의 수입니다.
- 인접 리스트를 사용할 때 \(O(V+E)\)
- 인접 행렬을 사용할 때 \(O(V^2)\)
응용
- 선수 과정 표현
- 컴파일 작업 순서 결정
- 버전 히스토리 관리
ex) git - 교착상태 탐지 등등




