Naive Pattern Searching 알아보기
naive pattern searching은 패턴 검색 알고리즘 중에서 가장 간단한 알고리즘입니다.
단순히 문자를 처음부터 끝까지 하나하나 비교해가며 패턴을 찾기 때문에 작은 문자열에서 패턴을 찾을 때 유용합니다.
구현
길이가 n인 텍스트 T안에 모든 위치에서 길이가 m인 패턴 P와 매치 여부를 검토합니다.
패턴의 길이는 텍스트의 길이보다 작거나 같아야 합니다. (m ≤ n)
- T[0 ... n-1]
- P[0 ... m-1]
패턴 P는 텍스트 T의 처음부터 n-m+1까지 이동하며 매치가 되는지 검토합니다.
패턴이 발견되면 패턴의 위치를 출력하고 다음 일치 위치를 찾습니다.
구현하면 다음과 같습니다.
void naivePatternSearch (char T[], char P[]) {
int n = strlen(T);
int m = strlen(P);
for (int i = 0; i <= n-m; i++) {
for (int j = 0; j < m; j++) {
if (T[i+j] != P[j])
break;
}
if (j == m)
printf("Pattern found at index %d \n", i);
}
}Input & Output
Input:
T[] = "AABAAAB"
P[] = "AA"
Output:
Pattern found at position 0
Pattern found at position 3
Pattern found at position 4
그림 설명
길이가 7인 텍스트와 길이가 2인 패턴을 가지고 패턴 위치를 찾는 과정을 보겠습니다.
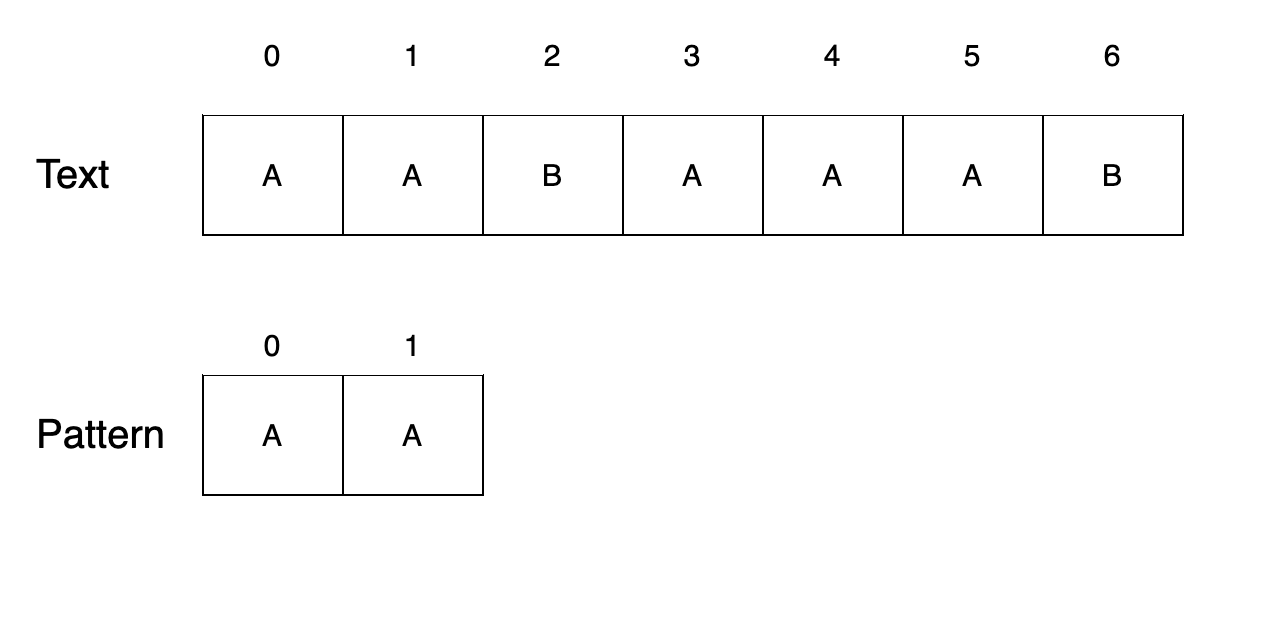
Step 1
텍스트 0번째 위치에서 패턴을 찾습니다. 위치를 출력하고 다음 위치로 이동합니다.
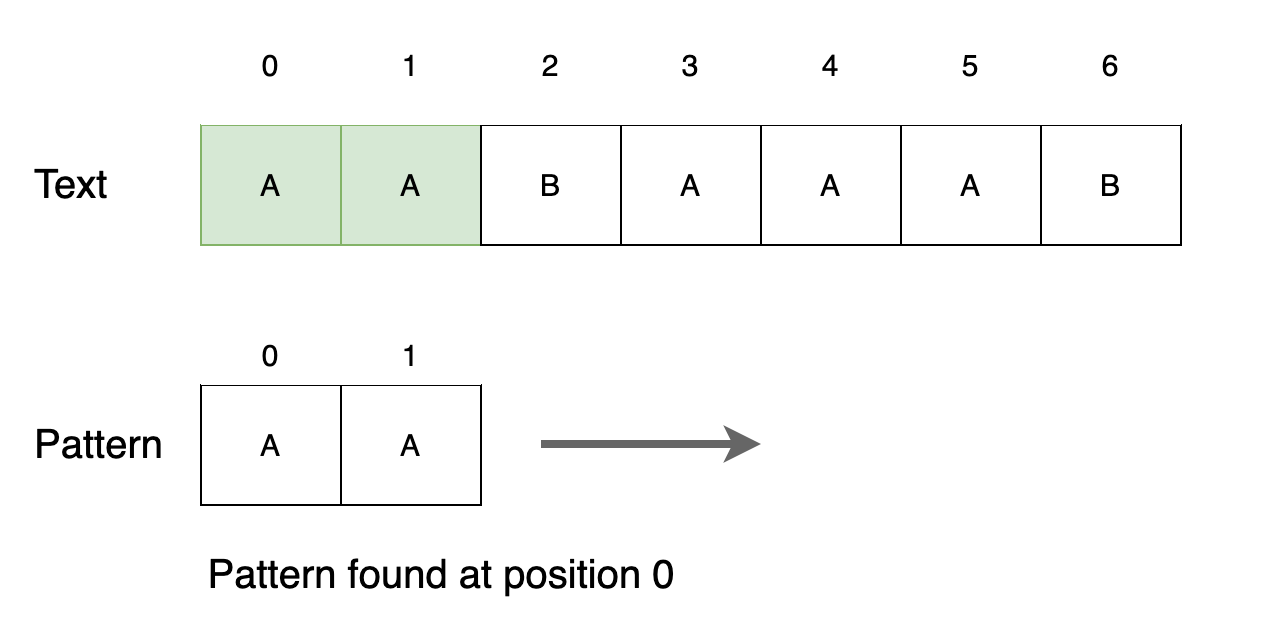
Step 2
텍스트 첫 번째 위치에서 패턴을 찾지 못합니다. 다음 위치로 이동합니다.
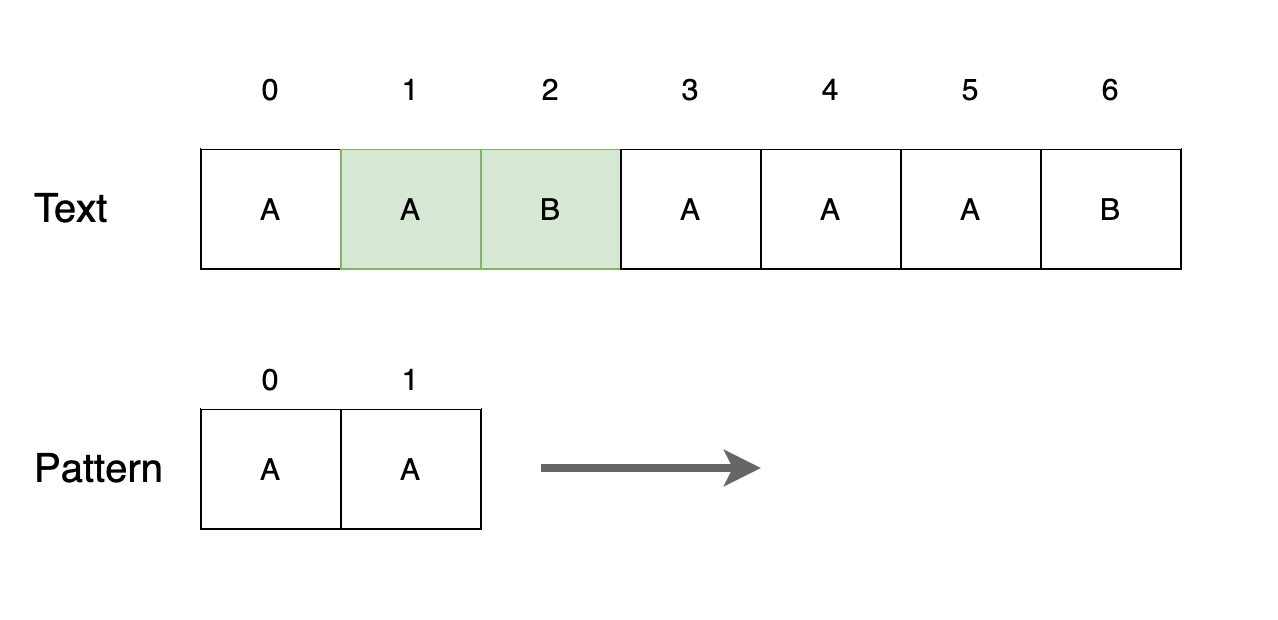
Step 3
텍스트 두 번째 위치에서 패턴을 찾지 못합니다. 다음 위치로 이동합니다.
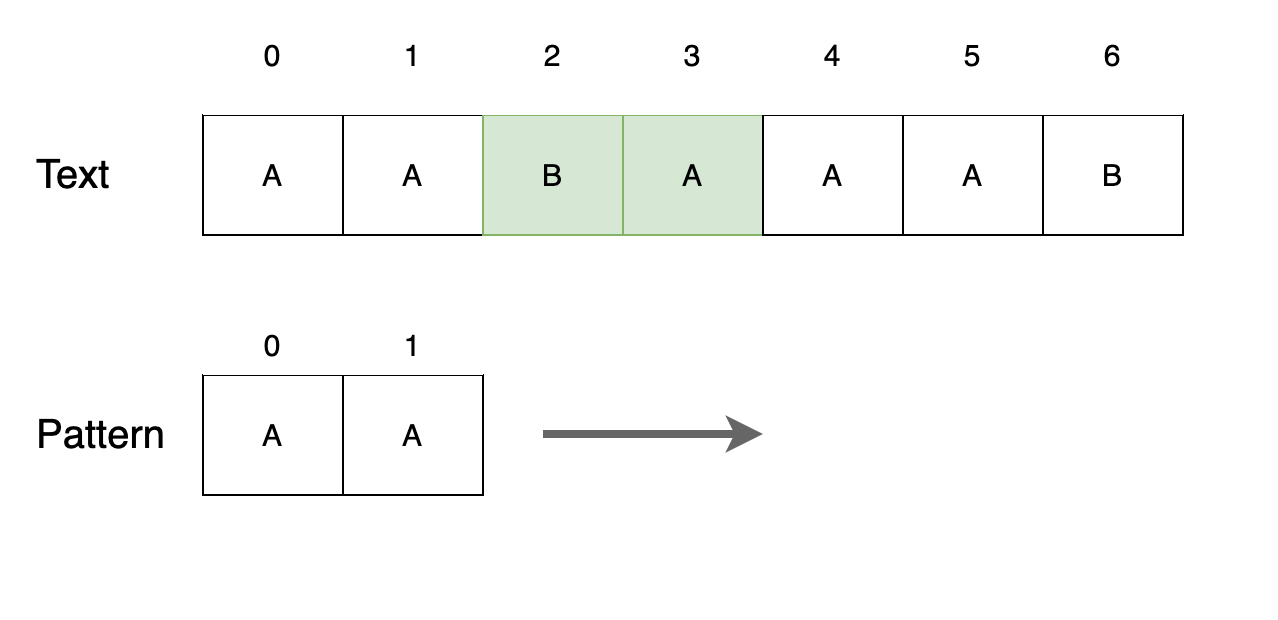
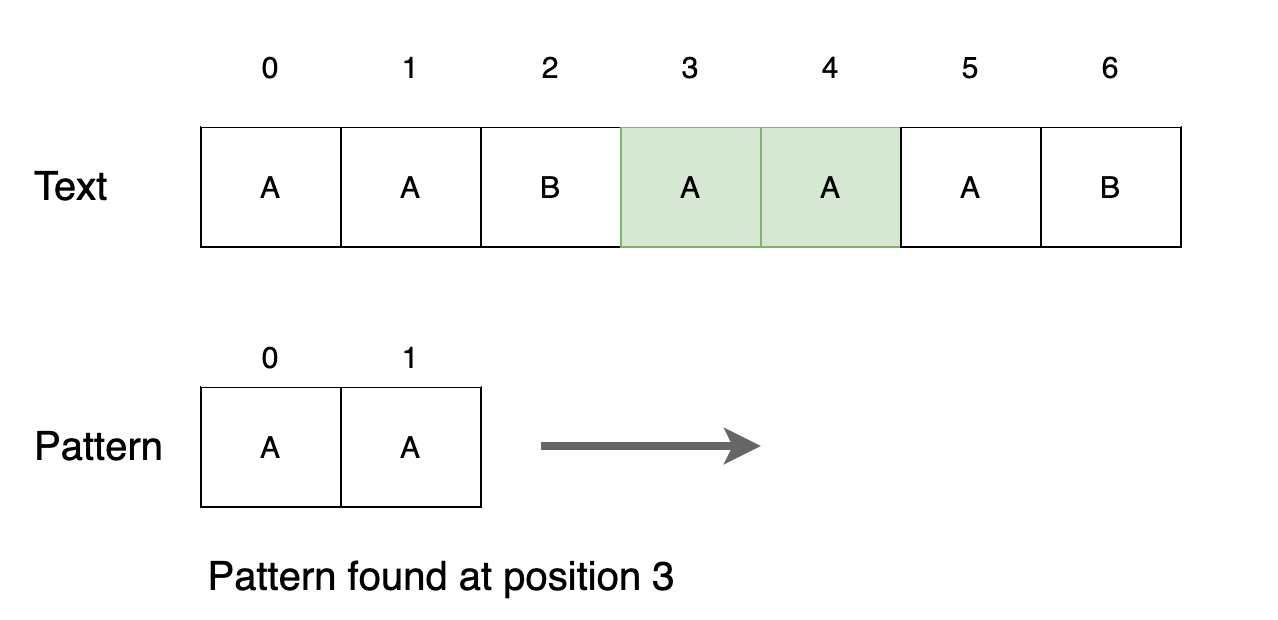
Step 4
텍스트 세 번째 위치에서 패턴을 찾습니다. 위치를 출력하고 다음 위치로 이동합니다.
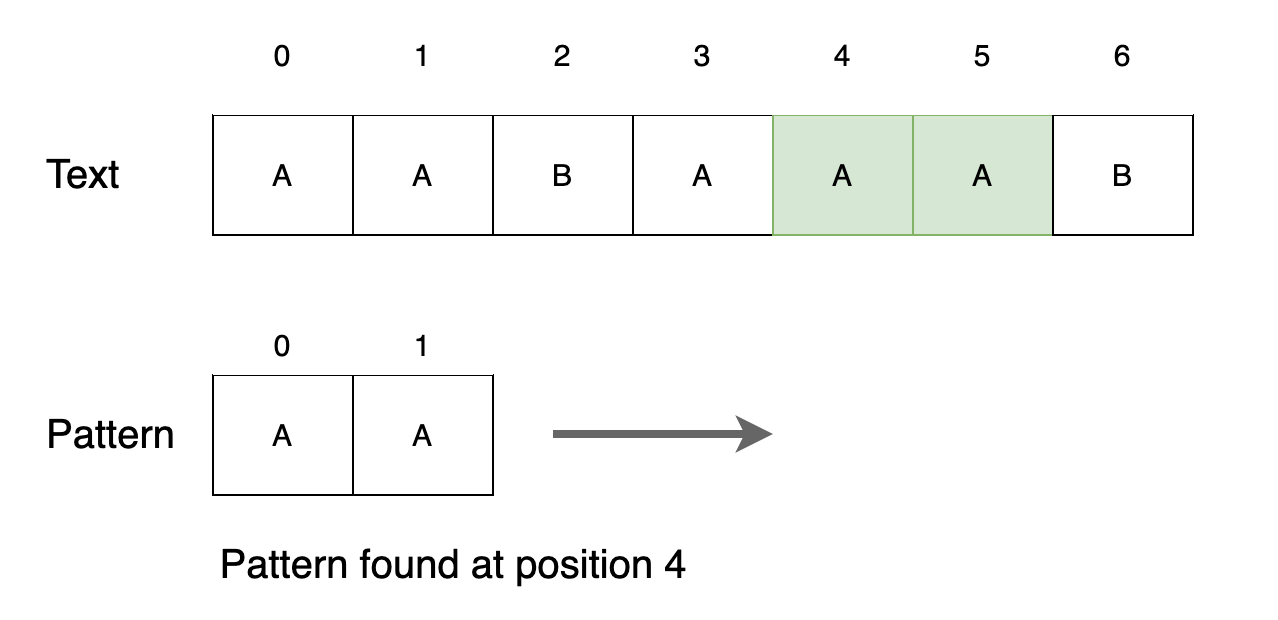
Step 5
텍스트 네 번째 위치에서 패턴을 찾습니다. 위치를 출력하고 다음 위치로 이동합니다.
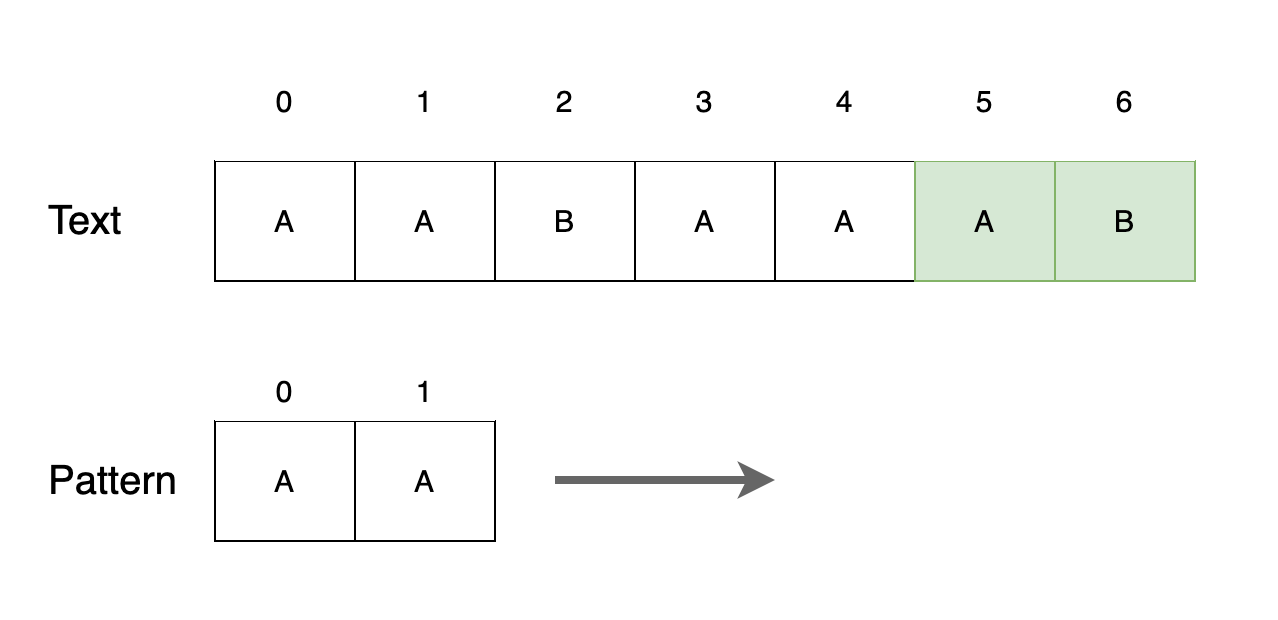
Step 6
텍스트 다섯 번째 위치에서 패턴을 찾지 못합니다. 모든 위치를 이동했기 때문에 종료합니다.
장단점
장점
- 실행 시간이 일치 시간과 같기 때문에 전처리 단계가 필요하지 않습니다.
- 추가 공간이 필요하지 않습니다.
단점
- 하나하나 비교하기 때문에 비효율 적입니다.
성능
Best case
Text [] = "AABAAAB"
Pattern [] = "FAA"
- 패턴의 첫 문자가 텍스트에 없을 때 가장 좋습니다.
- 텍스트의 길이를 n이라고 했을 최상의 경우 시간 복잡도는 \(O(n)\) 입니다.
Worst case
1. 텍스트와 패턴의 모든 문자가 같을 경우 최악의 케이스가 됩니다.
Text [] = "AAAAAAA"
Pattern [] = "AAA"
2. 패턴의 마지막 문자만 다른 경우에도 최악의 케이스가 됩니다.
Text [] = "AAAAAAA"
Pattern [] = "AAB"
최악의 경우 시간 복잡도는 다음과 같습니다.
\( O(m*(n-m+1)) \) (m은 패턴의 길이, n은 텍스트의 길이)




