[자료구조] 트리 순회 (Tree Traversal)

목차

 

트리 순회 (Tree Traversal)

---

트리의 모든 노드들을 방문하는 과정을 트리 순회(TreeTraversal)라고 합니다.

선형 자료 구조(연결 리스트, 스택, 큐 등)는 순차적으로 요소에 접근하지만 트리 자료구조는 다른 방식을 사용해야 합니다.

 

일반적으로 트리 순회에는 다음과 같은 방법들이 있습니다.

• 전위 순회 (Preorder)
• 중위 순회 (Inorder)
• 후위 순회 (Postorder)

이러한 순회는 보통 재귀로 쉽게 구현할 수 있습니다.

전위 순회 (Preorder Traversal)

---

전위 순회는 깊이 우선 순회(DFT, Depth-First Traversal)이라고도 합니다.

 

트리를 복사하거나, 전위 표기법을 구하는데 주로 사용됩니다.

트리를 복사할때 전위 순회를 사용하는 이유는 트리를 생성할 때 자식 노드보다 부모 노드가 먼저 생성되어야 하기 때문입니다.

 

전위 순회는 다음과 같은 방법으로 진행합니다.

1. Root 노드를 방문한다.
2. 왼쪽 서브 트리를 전위 순회한다.
3. 오른쪽 서브 트리를 전위 순회한다.

Preorder Traversal

위 트리에 전위 순회 결과는 다음과 같습니다.

A→B→D→E→C→F→G

구현

struct node {
  char data;
  struct node *left;
  struct node *right;
} Node;

void printPreorder (Node *root) {
  // 노드가 없다면 종료한다.
  if (root == NULL)
    return;

  // root data를 출력(방문)한다.
  printf("%c ", root->data);
  
  // 왼쪽 서브트리로 재귀한다.
  printPreorder(root->left);
  
  // 오른쪽 서브트리로 재귀한다.
  printPreorder(root->right);
}

Output:

A B D E C F G

728x90

중위 순회 (Inorder Traversal)

---

중위 순회는 왼쪽 오른쪽 대칭 순서로 순회를 하기때문에 대칭 순회(symmetric traversal)라고도 합니다.

 

중위 순회는 이진 탐색트리(BST)에서 오름차순 또는 내림차순으로 값을 가져올 때 사용됩니다.

내림차순으로 값을 가져오기 위해서는 역순(오른쪽-> root-> 왼쪽)으로 중위 순회를 하면 됩니다.

 

중위 순회는 다음과 같은 방법으로 진행합니다.

1. 왼쪽 서브 트리를 중위 순회한다.
2. Root 노드를 방문한다.
3. 오른쪽 서브 트리를 중위 순회한다.

Inorder Traversal

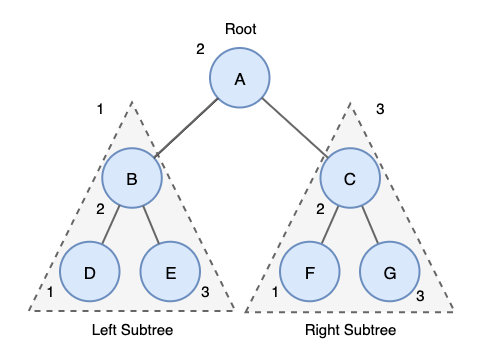
위 트리에 중위 순회 결과는 다음과 같습니다.

D→B→E→A→F→C→G

구현

struct node {
  char data;
  struct node *left;
  struct node *right;
} Node;

void printInorder (Node *root) {
  // 노드가 없다면 종료한다.
  if (root == NULL)
    return;

  // 왼쪽 서브트리로 재귀한다.
  printInorder(root->left);

  // root data를 출력(방문)한다.
  printf("%c ", root->data);
  
  // 오른쪽 서브트리로 재귀한다.
  printInorder(root->right);
}

Output:

D B E A F C G

후위 순회 (Postorder Traversal)

---

후위 순회는 트리를 삭제하는데 주로 사용됩니다.

이유는 부모노드를 삭제하기 전에 자식 노드를 삭제하는 순으로 노드를 삭제해야 하기 때문입니다.

 

후위 순회는 다음과 같은 방법으로 진행합니다.

1. 왼쪽 서브 트리를 후위 순회한다.
2. 오른쪽 서브 트리를 후위 순회한다.
3. Root 노드를 방문한다.

Postorder Traversal

위 트리에 중위 순회 결과는 다음과 같습니다.

D→E→B→F→G→C→A

구현

struct node {
  char data;
  struct node *left;
  struct node *right;
} Node;

void printPostorder (Node *root) {
  // 노드가 없다면 종료한다.
  if (root == NULL)
    return;

  // 왼쪽 서브트리로 재귀한다.
  printPostorder(root->left);

  // 오른쪽 서브트리로 재귀한다.
  printPostorder(root->right);

  // root data를 출력(방문)한다.
  printf("%c ", root->data);
}

Output:

D E B F G C A