알고리즘

최단 경로 문제: 다익스트라 알고리즘 (Dijkstra's Algorithm)

yoongrammer 2021. 9. 16. 19:42
728x90

목차

    다익스트라 알고리즘 (Dijkstra's Algorithm) 알아보기

    다익스트라(Dijkstra) 알고리즘은 최단 경로(Shortest path) 문제 중에 Single-source path 찾는 알고리즘입니다.

     

    최단 경로 문제는 아래 글을 참고하시기 바랍니다.

    https://yoongrammer.tistory.com/87

     

    최단 경로(Shortest path) 문제 개념

    목차   최단 경로(Shortest path) 문제 알아보기 최단 경로 문제(shortest-paths proble)란 두 노드를 잇는 가장 짧은 경로를 찾는 문제입니다. 여기서 가장 짧은 경로란 간선의 가중치 합이 가장 작은 경로

    yoongrammer.tistory.com

     

    특징

    • 음수 가중치를 가진 간선이 없어야 합니다.
    • 탐욕 알고리즘(greedy algorithm)을 사용합니다.
    • 미방문 정점들을 저장하기 위해 우선순위 큐를 사용합니다.

    구현

    다익스트라 알고리즘은 우선순위 Queue를 사용하는 BFS (Breadth-First Search) 알고리즘과 비슷합니다.

     

    의사 코드는 다음과 같습니다.

    • S = 방문한 정점들의 집합
    • Q = 방문하지 않은 정점들을 저장하고 있는 우선순위 큐
    DIJKSTRA(G, w, s)
1  INITIALIZE-SINGLE-SOURCE(G,s)
2  S ← ∅
3  Q ← V [G]
4  while Q != ∅
5    do u ← Extract-Min(Q)
6    S ← S ∪ {u}
7    for each vertex v ∈ Adj[u]
8      do Relax(u, v, w)
    1. 그래프(G)에 있는 모든 정점을 초기화합니다.
      모든 정점은 d[v] = ∞ 로 초기화 되고 그중 시작 정점인 s는 0으로 초기화 합니다.
    2. 집합 S를 초기화 합니다.
    3. 우선순위 큐(Q)에 그래프에 있는 모든 정점을 저장합니다.
    4. 큐가 빌때까지 다음 작업을 진행합니다.
      1. 우선순위 큐에서 가장 작은 d값을 가진 정점 u를 가져옵니다.
        (d : 시작 정점부터 현재 정점까지의 최단경로 측정치)
      2. 정점 u를 집합 S에 넣습니다.
      3. 정점 u와 인접한 정점들에 Relax 연산을 수행합니다.

    INITIALIZE-SINGLE-SOURCE, Relax 연산에 대해서는 위 링크에 있는 최단경로 문제 개념을 참고하시기 바랍니다.

    728x90

     

    그림 예시

    1. 모든 정점을 초기화 합니다. 각 정점의 값은 d[v] 값입니다.

    • 시작 정점을 s라고 했을때 d[s]=0으로하고 나머지 정점의 d[v]값은 무한대로 초기화 합니다.
    • Queue에 방문하지 않은 정점들을 넣습니다.
    Step 1

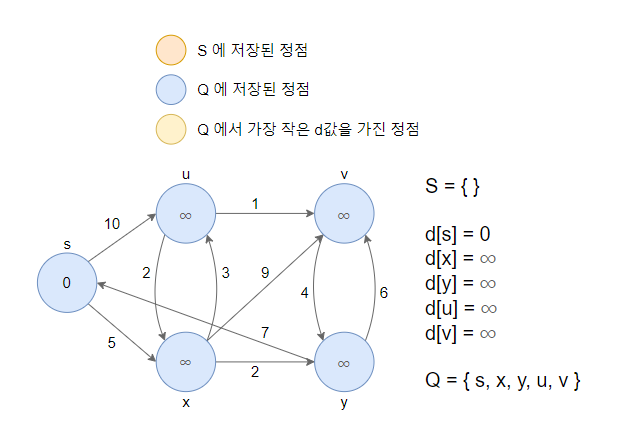
    2. 거리가 최소인 정점 s를 큐에서 제거하고, 그 노드를 방문했다는 의미로 S집합에 추가합니다. 이후 인접한 정점(u, x)과 RELAX연산을 수행합니다.

     

    Step 2

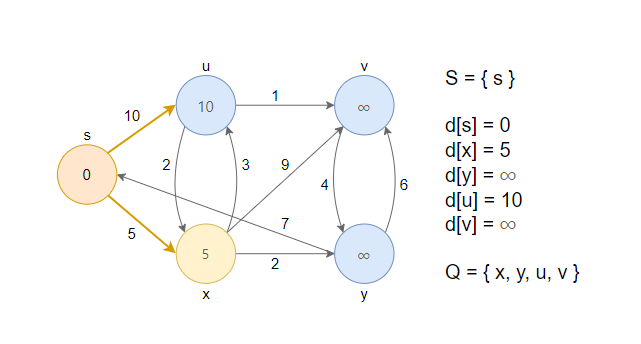
    3. 거리가 최소인 정점 x를 큐에서 제거하고, 그 노드를 방문했다는 의미로 S집합에 추가합니다. 이후 인접한 정점(u, v, y)과 RELAX연산을 수행합니다.

    Step 3

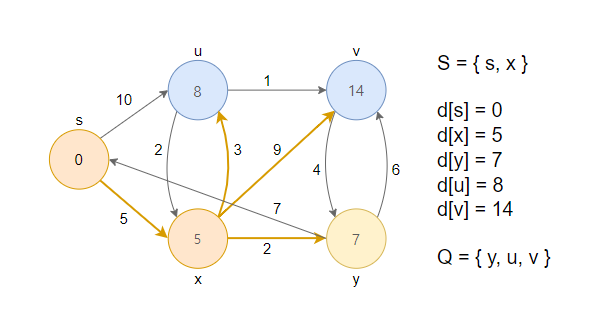
    4. 거리가 최소인 정점 y를 큐에서 제거하고, 그 노드를 방문했다는 의미로 S집합에 추가합니다. 이후 인접한 정점(s, v)과 RELAX연산을 수행합니다.

    Step 4

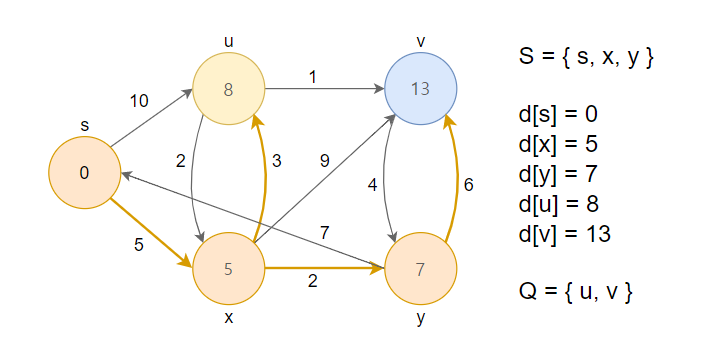
    5. 거리가 최소인 정점 u를 큐에서 제거하고, 그 노드를 방문했다는 의미로 S집합에 추가합니다. 이후 인접한 정점(x, v)과 RELAX연산을 수행합니다.

    Step 5

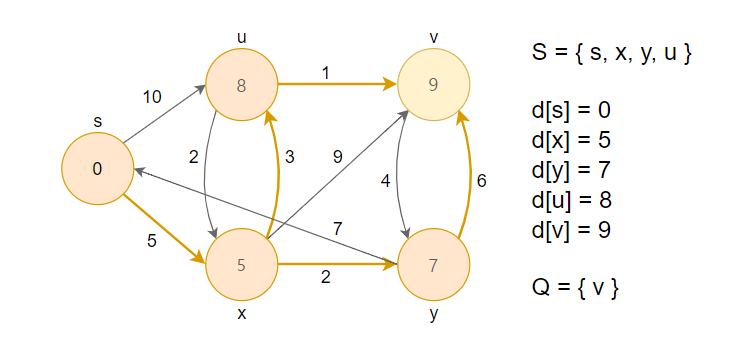
    6. 거리가 최소인 정점 v를 큐에서 제거하고, 그 노드를 방문했다는 의미로 S집합에 추가합니다. 이후 인접한 정점(y)과 RELAX연산을 수행합니다.

    Step 6

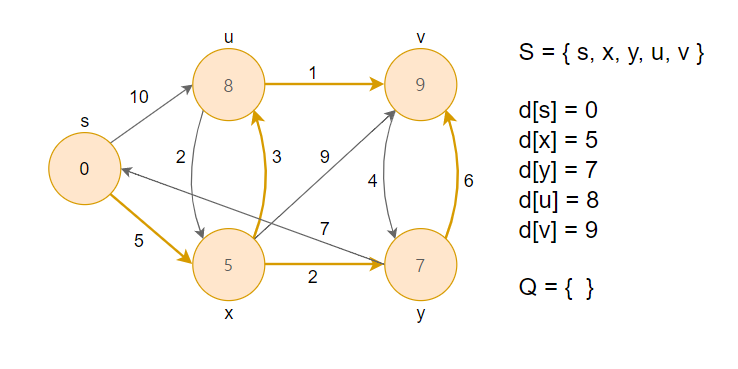
    최종적으로 주황색 간선이 시작 정점 s에서 각 정점까지의 최단 경로가 됩니다.

     

    성능

    다익스트라 알고리즘의 성능은 우선순위 큐를 어떻게 구현하느냐에 따라 다릅니다.

    V는 정점의 수이고 E는 간선의 수 입니다.

     

    우선순위 큐를 배열로 구현했을 때

    Extract-Min(Q) 작업에는 \(O(V)\) 시간이 소요되고 총 V번 호출하기 때문에 총 Extract-Min의 연산은 \(O(V^2)\)의 시간이 소요됩니다.

    RELAX연산은 \(O(1)\) 시간이 소요되고 총 E번 호출하기 때문에 총 RELAX연산은 \(O(E)\)의 시간이 소요됩니다.

    그러므로 다익스트라 알고리즘의 시간 복잡도는 \(O(V^2 + E) = O(V^2)\)입니다.

    우선순위 큐를 이진 힙(binary heap)으로 구현했을 때

    Extract-Min(Q) 작업에는 \(O(logV)\) 시간이 소요되고 총 V번 호출하기 때문에 총 Extract-Min의 연산은 \(O(VlogV)\)의 시간이 소요됩니다.

    이진 힙인 경우 RELAX연산에서 DECREASE-KEY를 호출하기 때문에 \(O(logV)\)의 시간이 소요되고 총 E번의 RELAX연산을 수행하므로 \(O(ElogV)\)의 시간이 소요됩니다.

    그러므로 시간복잡도는 \(O(VlgV+ElgV) = O((V+E) logV)\)입니다.

     

    그래프가 connected라면 최소한 정점수만큼 간선이 있기 때문에 \(O(ElogV)\)로 단순화할 수 있습니다.

    다익스트라 알고리즘은 벨만 포드 알고리즘의 \(O(EV)\) 보다 더 빠릅니다.

     

    728x90
    저작자표시 비영리 변경금지