최단 경로 문제: 플로이드 와셜 알고리즘 (Floyd-Warshall Algorithm)
목차
플로이드 와셜 알고리즘 (Floyd-Warshall Algorithm) 알아보기
플로이드 와셜 (Floyd-Warshall) 알고리즘은 최단 경로(Shortest path) 문제 중에 모든 정점 쌍(All-pairs)에 대해 최단 거리를 구하는 알고리즘입니다.
플로이드 와셜 알고리즘은 Floyd's algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, 또는 WFI algorithm 이라고도 합니다.
특징
- Dynamic Programming을 사용합니다.
- 유향 또는 무향 가중 그래프에서 최단 경로를 찾을 수 있으며 음수 사이클이 있는 경우는 찾지 못합니다.
- 그래프에 음수 사이클 여부를 확인할 수 있습니다.
구현
플로이드 와셜 알고리즘은 각각의 정점 쌍을 지나는 그래프의 모든 경로를 비교합니다.
플로이드 와셜 알고리즘은 Dynamic Programming을 사용하여 정점 i에서 j로 직접 가는 경로와 중간에 어느 정점을 거쳐 가는 경로를 비교하여 최단경로를 찾습니다.
이 방식으로 모든 정점 쌍에 대한 최단 거리를 구하게 됩니다.
다음은 중간에 노드 집합 {1,2,..., k}에 속한 노드들만 거쳐서 노드 i에서 j까지 가는 최단 경로의 길이를 의미합니다.
$$ d^k[i, j] $$
k= 0인 경우는 중간에 어떤 노드(k)도 거치지 않고 직접 정점 i에서 j까지 가는 경로를 의미하고, 만약 i에서 j까지 가는 경로가 존재하지 않는다면 무한대로 표시합니다.
$$ d^0[i, j] = \begin{cases} w_{ij}, & \mbox{if }(i, j) \in \mbox{E} \\ \infty, & \mbox{otherwise. } \end{cases} $$
중간에 노드 집합 {1,2,..., k}에 속한 노드들만 거쳐서 노드 i에서 j까지 가는 최단경로(\(d^k[i, j]\))는 두가지 경우가 있습니다.
- 노드 k를 지나는 경우 ( \(d^{k-1}[i, k] + d^{k-1}[k, j]\))
- 노드 k를 지나지 않는 경우 (\(d^{k-1} [i, j]\))
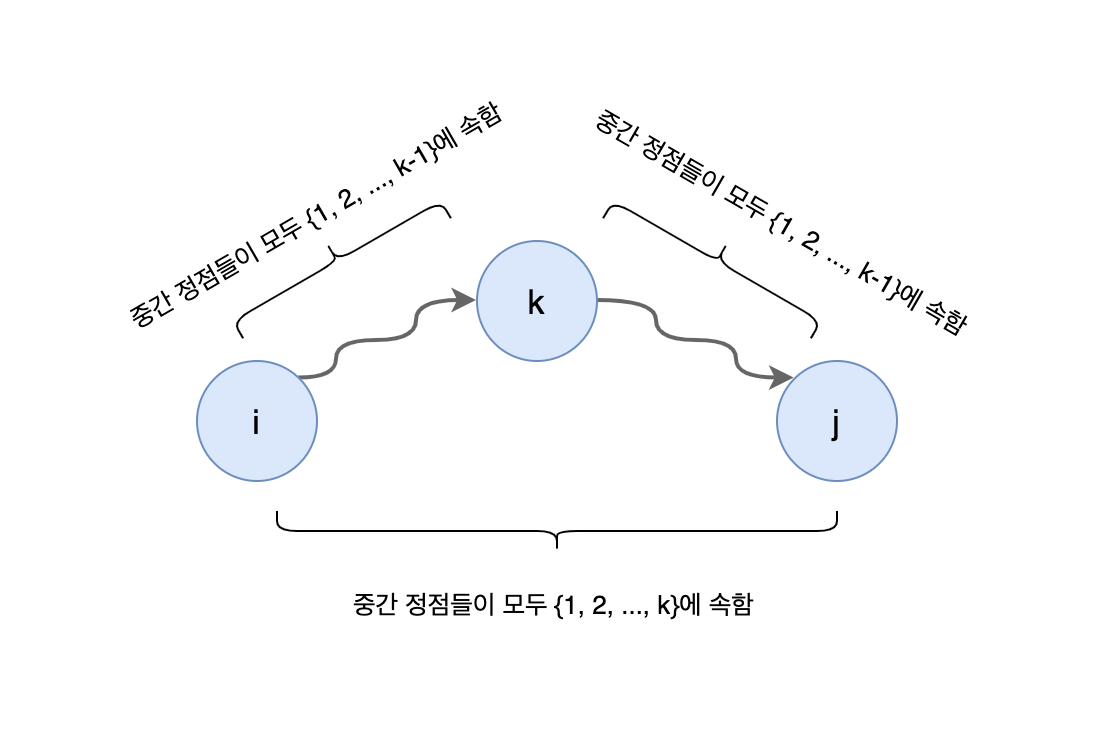
이중 짧은 경로가 최단 경로가 되며 다음과 같은 순환식을 얻을 수 있습니다.
$$ d^k[i, j] = min\{d^{k-1}[i, j], d^{k-1}[i,k] + d^{k-1}[k, j]\} $$
이 공식을 이용한 의사 코드는 다음과 같습니다.
// n = 정점의 수
// d = n*n 행렬
for i = 1 to n
for j = 1 to n
if i == j
d0[i, j] = 0
if (i, j) is an edge in E
d0[i, j] = wij
else
d0[i, j] =infinity
for k = 1 to n // 중간정점 집합
for i = 1 to n
for j = 1 to n
dk[i, j] = min (dk-1[i, j], dk-1[i, k] + dk-1[k, j])- 그래프의 내용을 \(d^0\)에 저장하는 초기화 작업을 진행합니다.
- 그다음 모든 (i, j) 쌍에 대해서 k=1일 때 \(d^k[i, j]\)를 계산하고, 다음으로 k=2일 때를 계산하는 식으로 k=n일 될 때까지 계속하면, 모든 (i, j)쌍에 대해서 최단 경로를 갖게 됩니다.
그림 예시
다음 그래프에서 최단 경로를 찾는 과정은 다음과 같습니다.
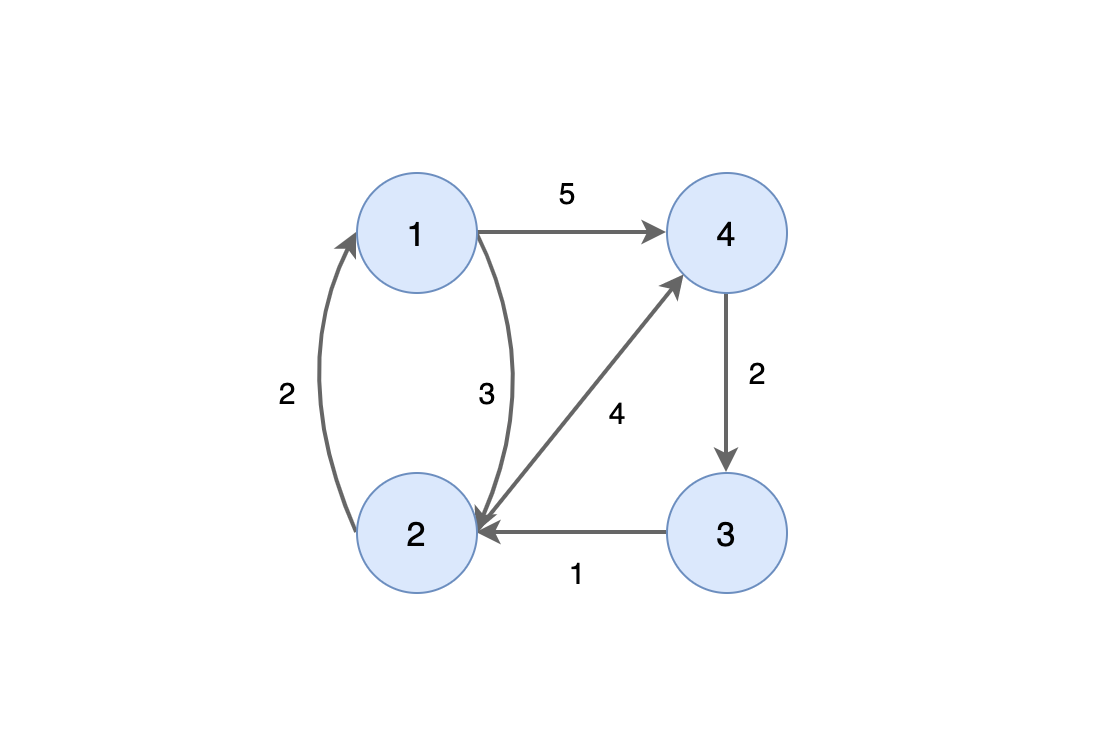
Step 1.
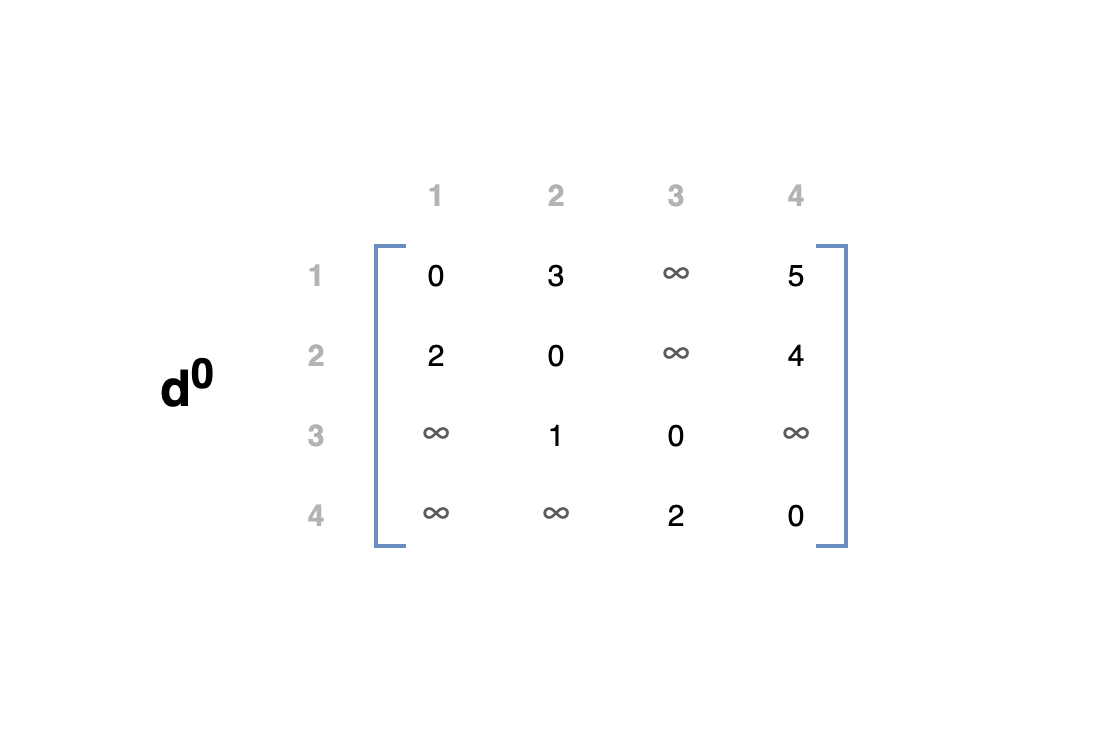
n * n 행렬 \(d^0\)에 그래프의 내용을 넣습니다.
- \(d^0[i][j]\) 는 그래프에서 i부터 j까지의 거리를 저장합니다. (i 와 j는 그래프의 정점입니다.)
- 경로가 없다면 무한대로 저장하고 자기 자신이라면 0으로 저장합니다.
Step 2.
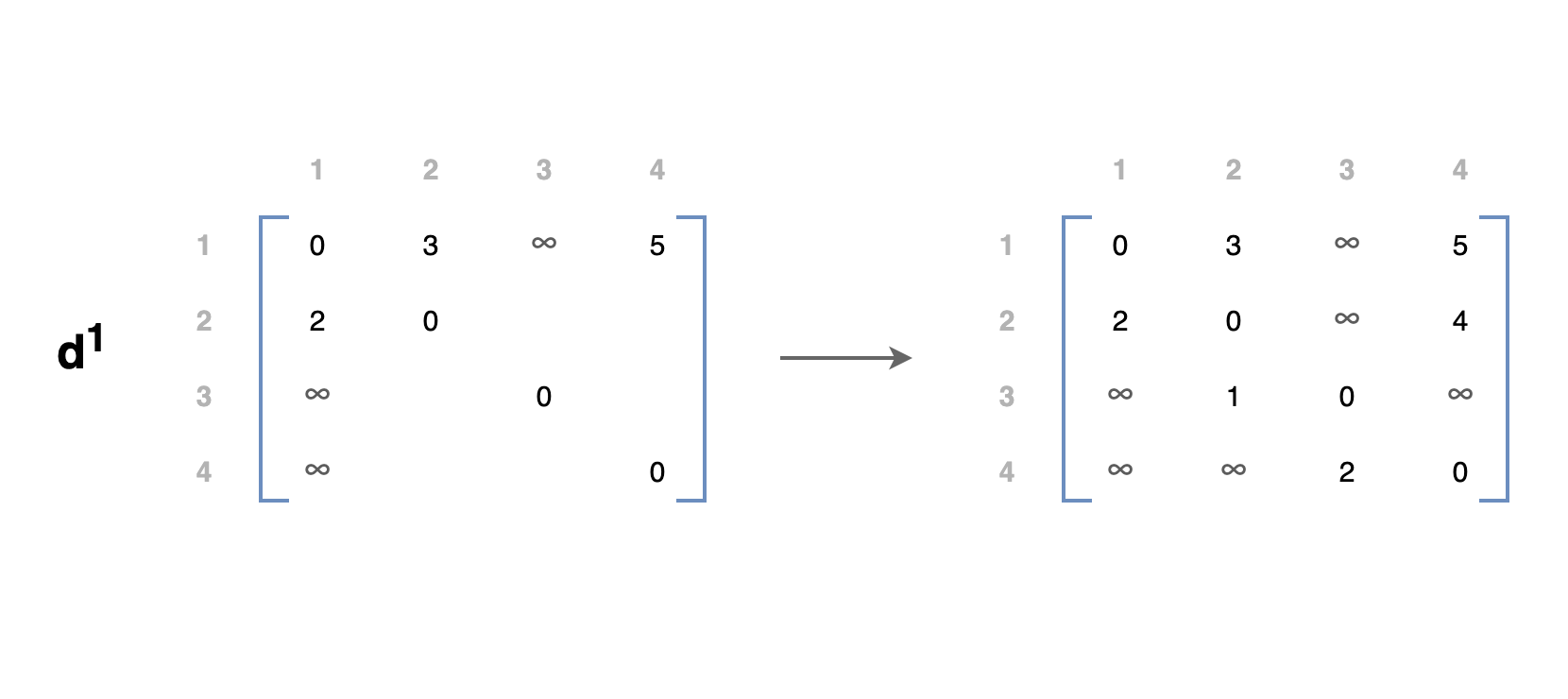
행렬 \(d^0\)를 사용하여 행렬 \(d^1\)을 만듭니다.
첫 번째 행과 열은 그대로 두고 나머지 셀은 다음 공식을 사용하여 채웁니다.
- k에 해당하는 행과 열은 공식을 사용해서 셀을 구해도 값이 변하지 않기 때문에 그림 설명 편의상 그대로 둔다고 표현함.
(k는 경로상의 중간 정점)
$$ d^k[i, j] = min\{d^{k-1}[i, j], d^{k-1}[i,k] + d^{k-1}[k, j]\} $$
예를 들어 \(d^1[3, 2]\) 값을 구한다면 다음과 같습니다.
$$ d^1[3 ,2] = min\{d^0[3, 2], d^0[3, 1] + d^0[1, 2]\} $$
$$ = min\{ 1, ∞ + 2\} = 1 $$
Step 3.
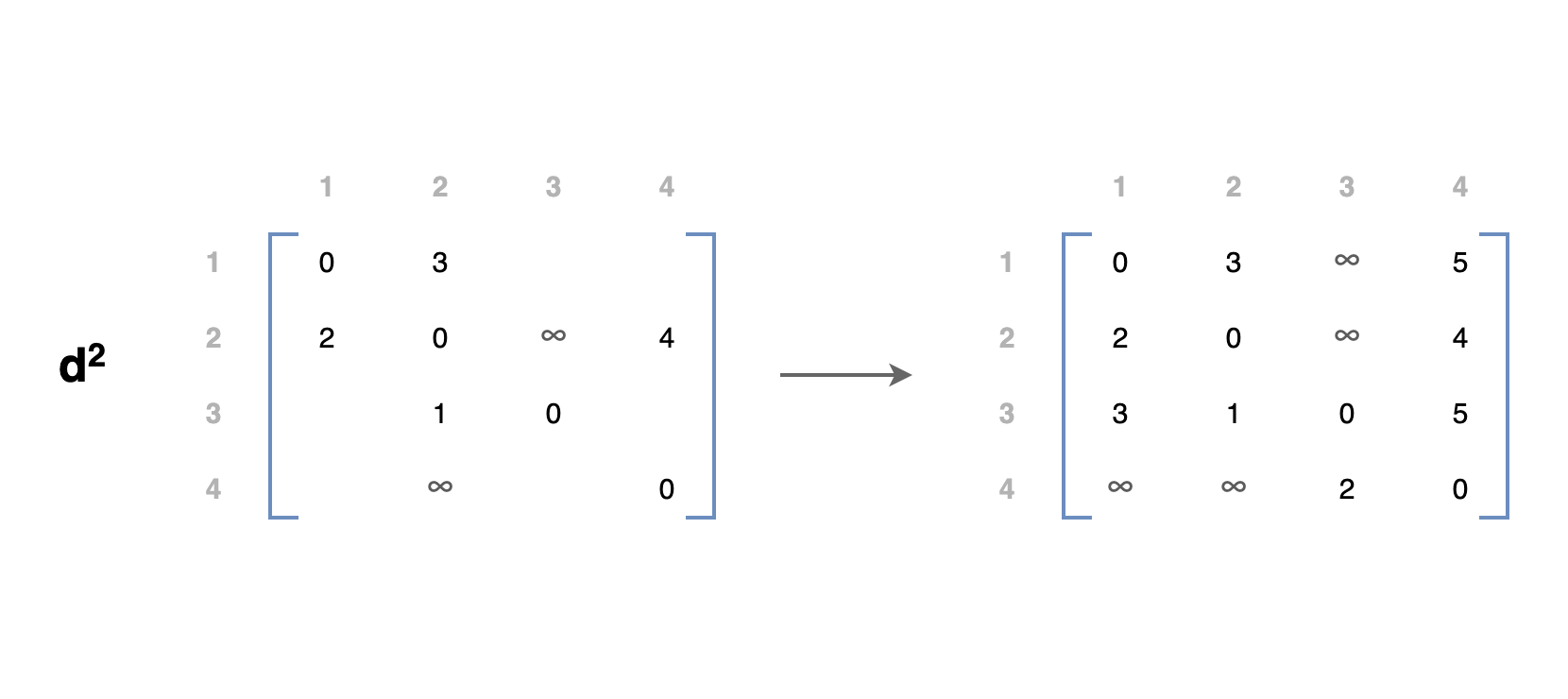
\(d^1\) 행렬을 사용하여 \(d^2\) 행렬을 채웁니다.
두 번째 행과 열은 그대로 두고 나머지는 Step 2. 와 유사하게 공식을 사용하여 셀을 채웁니다.
Step 4.
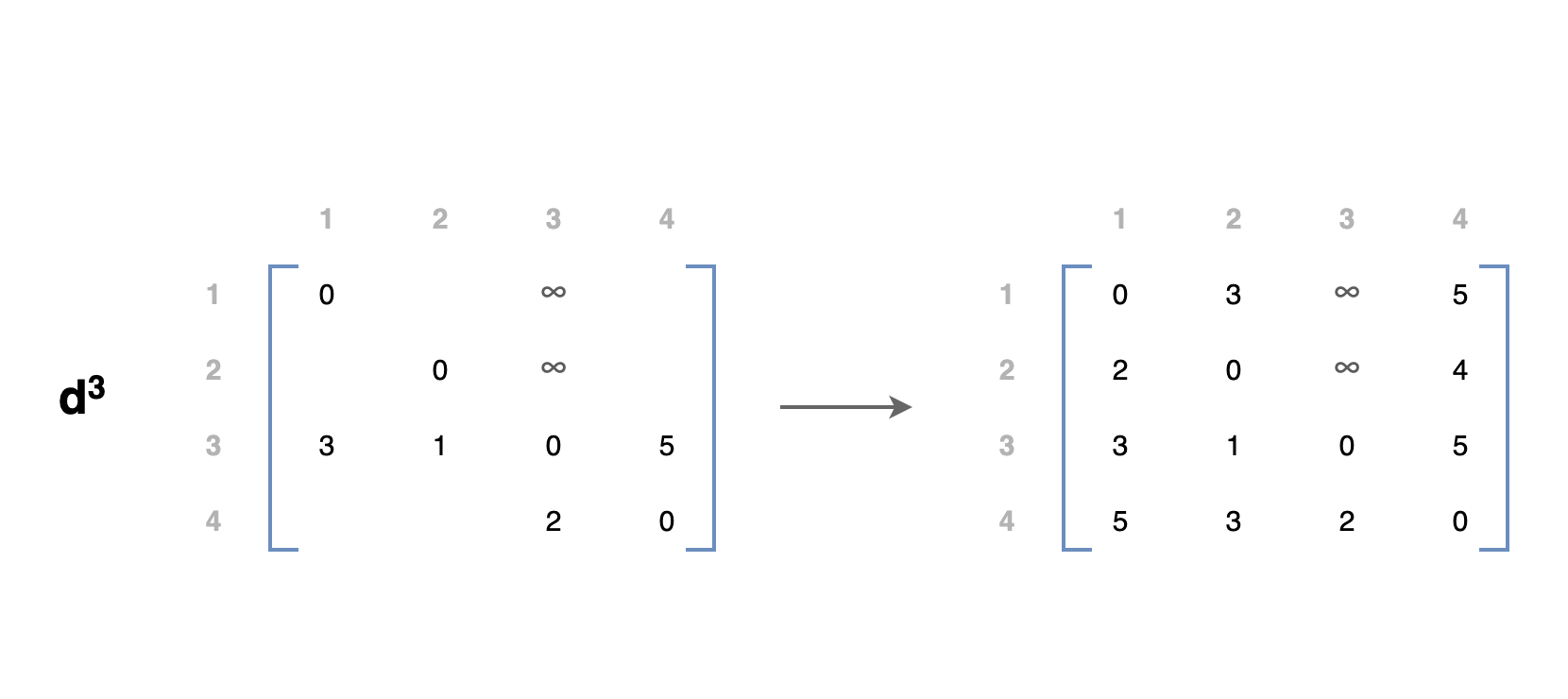
\(d^2\) 행렬을 사용하여 \(d^3\) 행렬을 채웁니다.
세 번째 행과 열은 그대로 두고 나머지는 Step 2. 와 유사하게 공식을 사용하여 셀을 채웁니다.
Step 5.
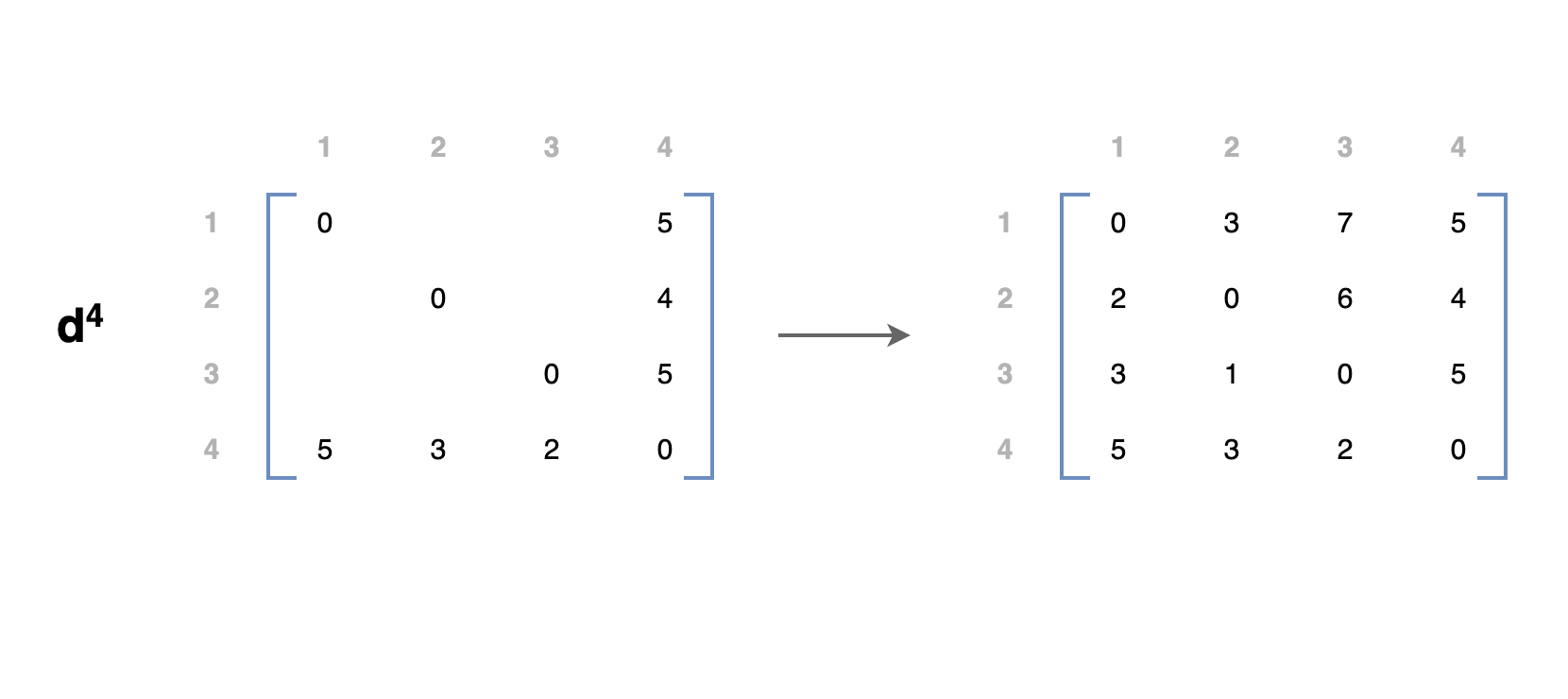
최종적으로 \(d^4\)는 모든 정점에 대한 최단경로가 저장된 행렬이 됩니다.
여기서 경로 (i, i)의 거리가 0보다 작게 된다면 음수 사이클이 존재한다는 것을 의미하게 됩니다.
성능
세 개의 중첩된 for문 때문에 \(O(|V|^3)\)의 시간이 걸립니다. (|V|는 정점의 수)
플로이드 와셜 알고리즘은 그래프의 정점 수에 의존하기 때문에 정점 수가 적은 그래프에서 사용하는 것이 좋습니다.