Lower bound & Upper bound 개념 및 구현
목차
Lower bound & Upper bound 개념 및 구현
Lower bound와 Upper bound는 경곗값을 찾는 알고리즘입니다.
Lower bound와 Upper bound는 이진 탐색을 기반으로 하기 때문에 데이터가 정렬되어 있어야 합니다.
이진 탐색을 기반으로 하기 때문에 두 알고리즘의 시간 복잡도는 O(log n) 입니다. (n: 배열 길이)
Lower bound
Lower bound는 특정 값의 시작 위치를 찾는 알고리즘입니다.
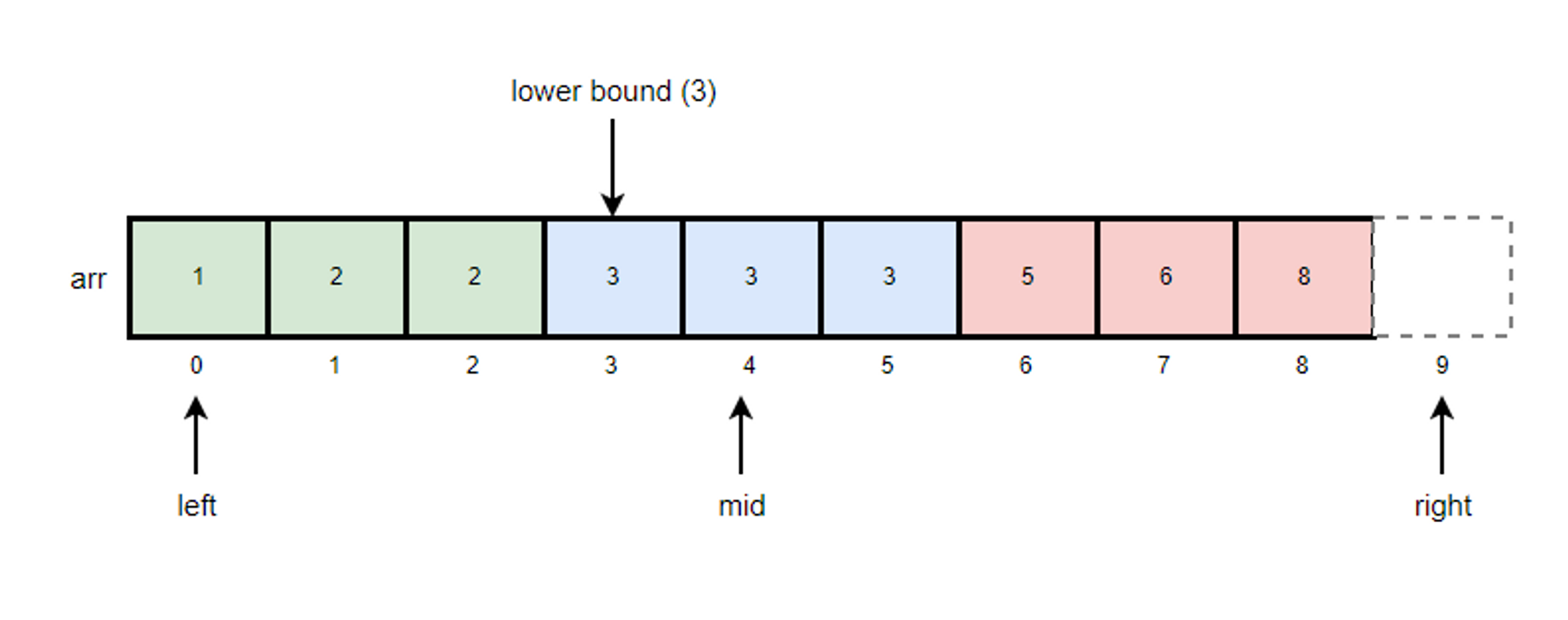
동작 방식
Lower bound의 동작 방식은 다음과 같습니다.
초기에 left는 배열의 시작 위치로 right는 배열의 길이로 셋팅합니다.
- 배열의 중간 값(mid)을 가져옵니다.
- 중간 값과 검색 값을 비교합니다.
- 중간 값이 검색 값보다 작다면 left 값을 mid+1로 합니다.
- 중간 값이 검색 값보다 크거나 같다면 right값을 mid로 합니다.
- left ≥ right 일 때까지 1번과 2번을 반복합니다.
- 반복이 끝나면 right 값이 lower bound가 됩니다.
다음은 arr 배열에서 k=3의 lower bound를 찾는 과정입니다.
1. mid 값을 구하고 k 값과 비교합니다.
- mid = (left + right)/2 = (0 + 9)/2 = 4
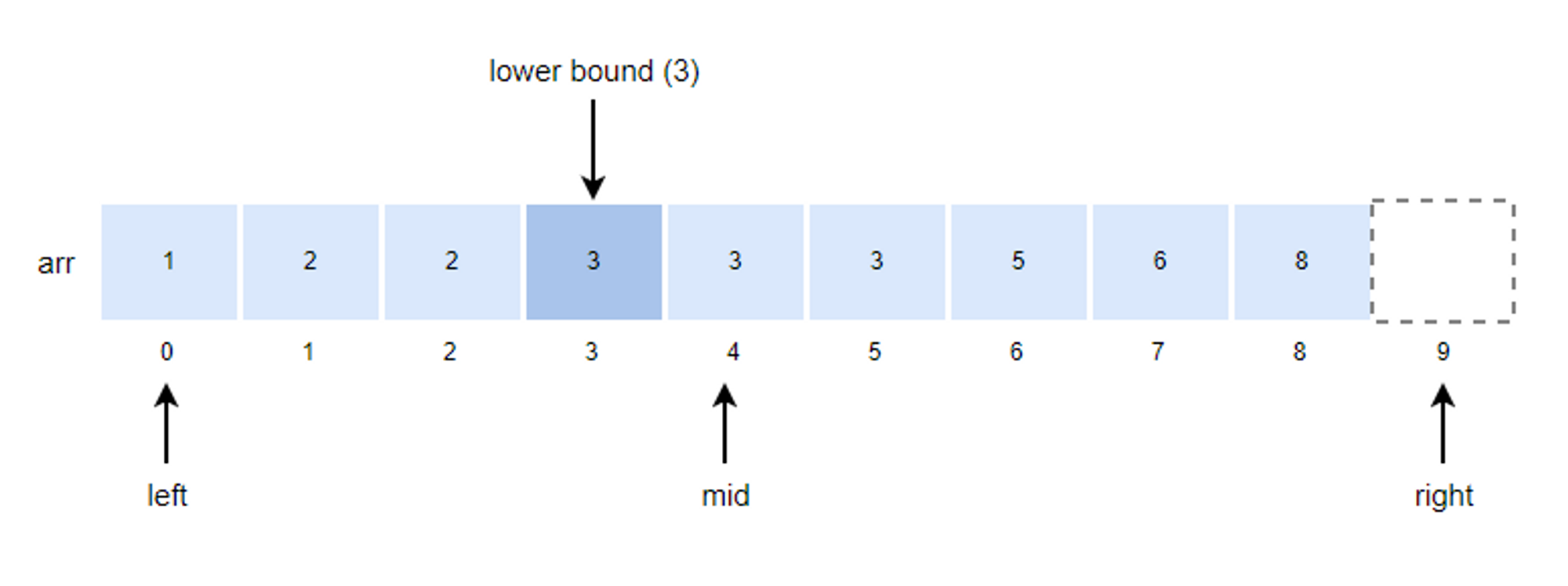
2. k값이 arr[mid]값과 같기 때문에 right의 위치를 mid로 변경합니다.
- right = mid = 4
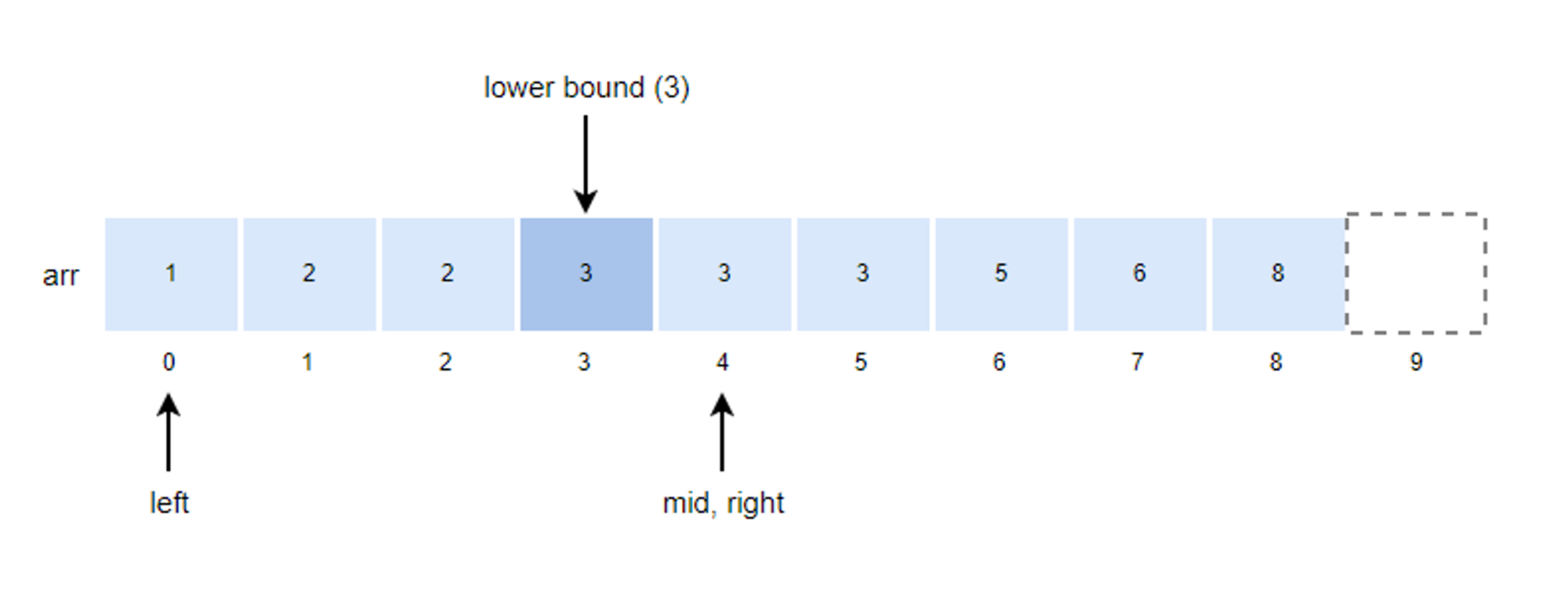
3. mid 값을 구하고 k 값과 비교합니다.
- mid = (left + right)/2 = (0 + 4)/2 = 2
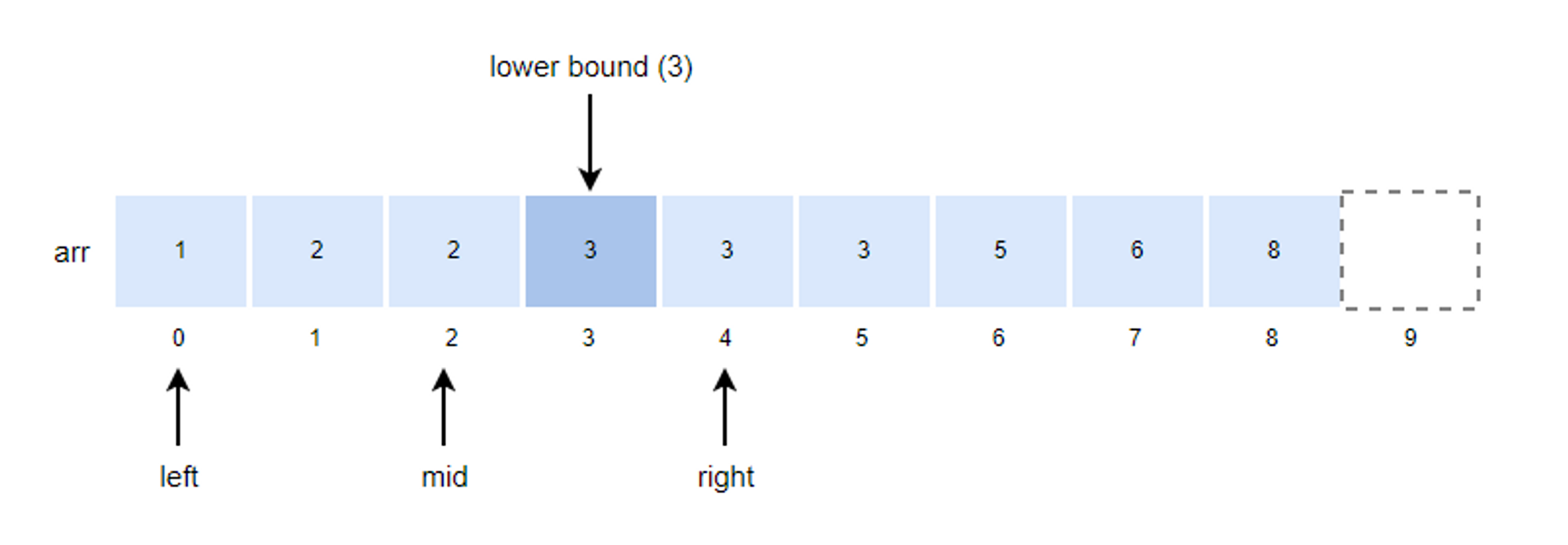
4. k값이 arr[mid]값보다 크기 때문에 left의 위치를 mid+1로 변경합니다.
- left = mid + 1 = 2 + 1 = 3
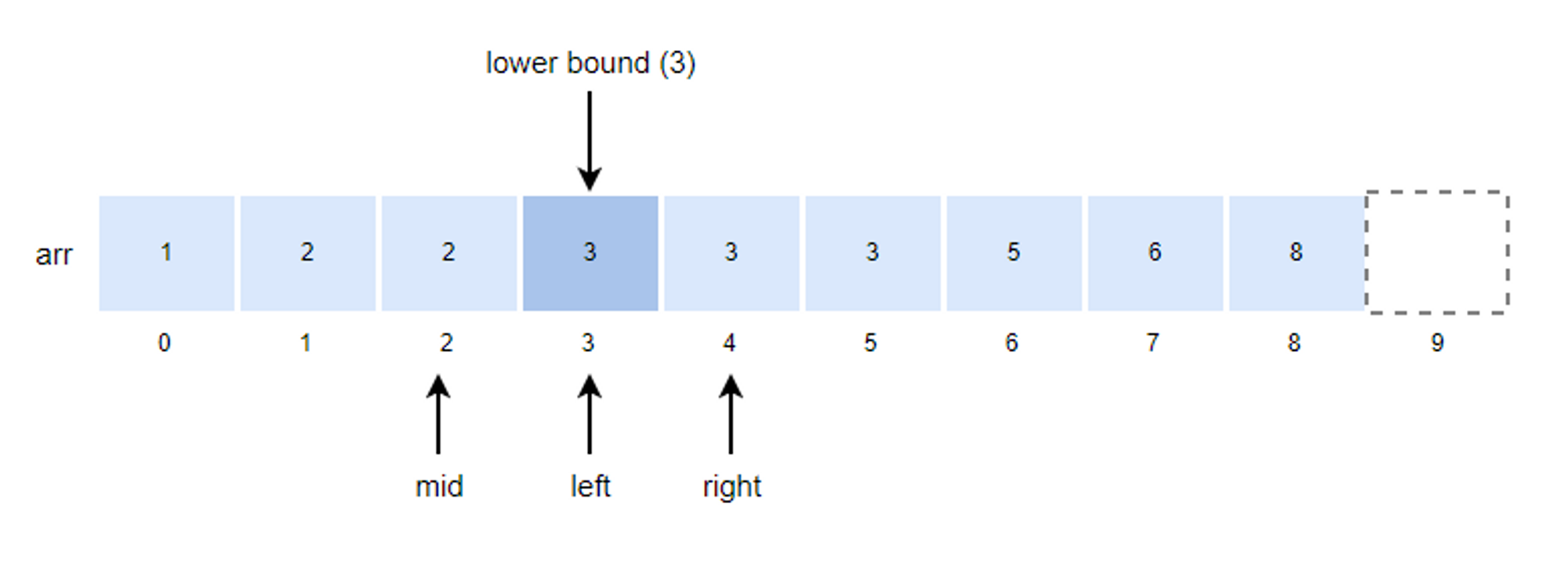
5. mid 값을 구하고 k값과 비교합니다.
- mid = (left + right)/2 = (3 +3)/2 = 3
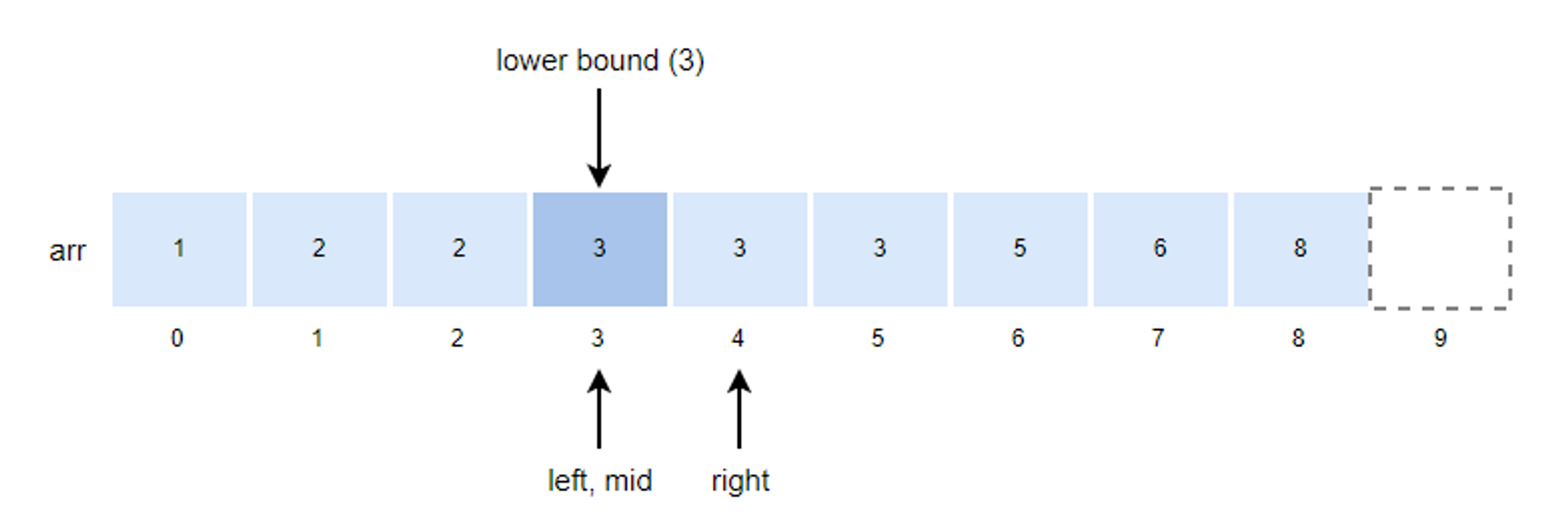
6. k값이 arr[mid]값과 같기 때문에 right의 위치를 mid로 변경합니다.
- right = mid = 3
- left값이 right 값과 같기 때문에 루프를 종료하고 right값이 lower bound 값이 됩니다.
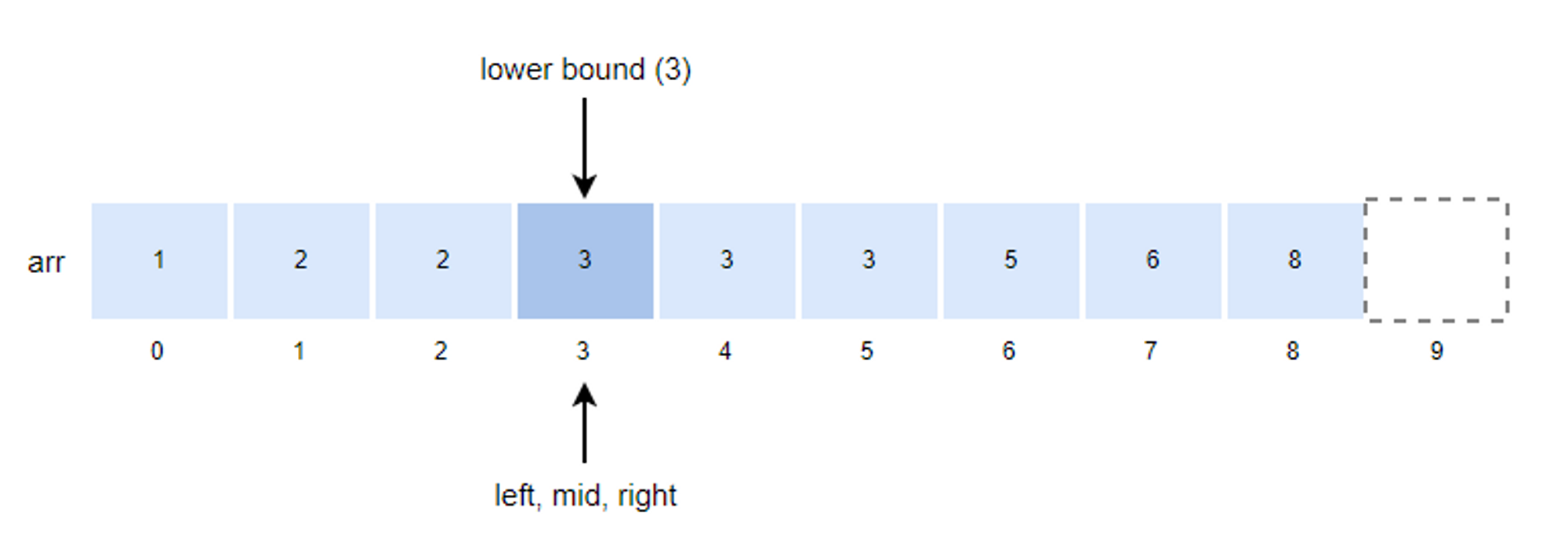
구현
다음은 arr배열에서 k값의 lower bound를 찾는 코드입니다.
- 매개변수로 left는 배열의 시작위치 right는 arr의 길이로 받습니다.
def lower_bound(arr, left, right, k):
while left < right:
mid = (left + right)//2
if arr[mid] < k:
left = mid + 1
else:
right = mid
return right
Upper bound
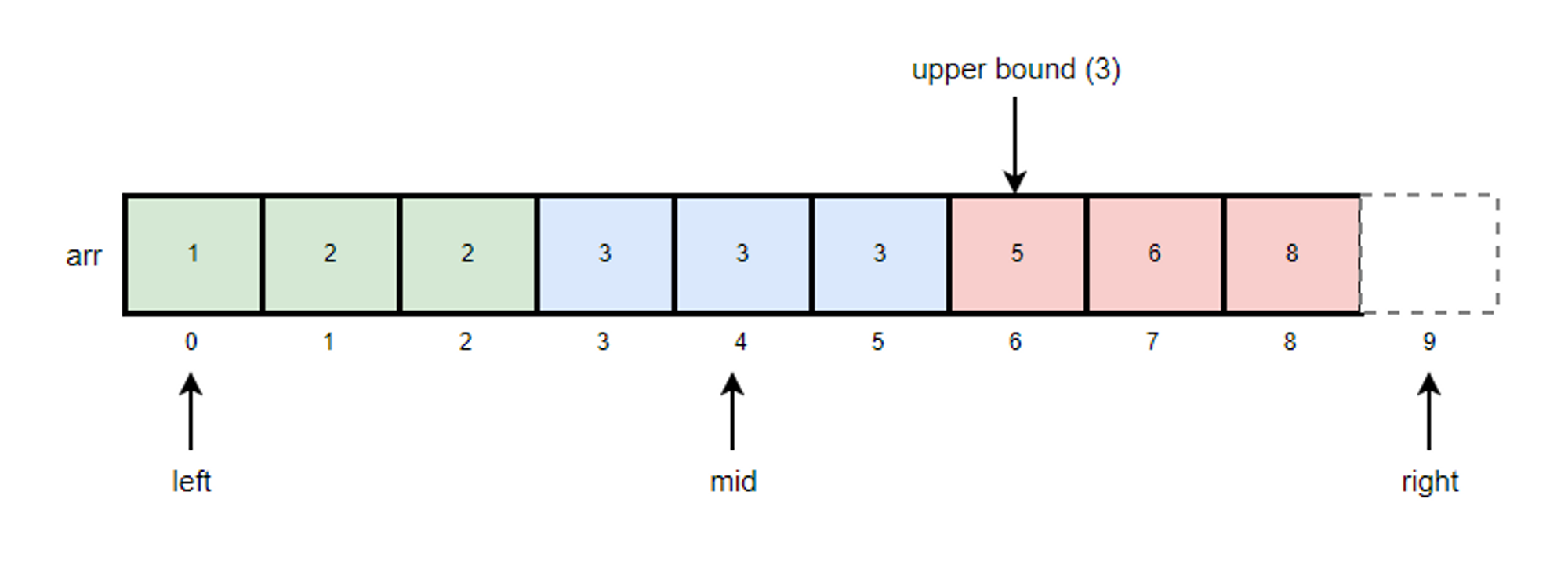
Upper Bound는 특정 k값보다 처음으로 큰 값의 위치를 찾는 알고리즘입니다.
동작 방식
Upper bound의 동작 방식은 다음과 같습니다.
초기에 left는 배열의 시작 위치로 right는 배열의 길이로 세팅합니다.
- 배열의 중간 값(mid)을 가져옵니다.
- 중간 값과 검색 값을 비교합니다.
- 중간 값이 검색 값보다 작거나 같다면 left 값을 mid+1로 합니다.
- 중간 값이 검색 값보다 크다면 right값을 mid로 합니다.
- left ≥ right 일 때까지 1번과 2번을 반복합니다.
- 반복이 끝나면 right 값이 upper bound가 됩니다.
다음은 arr 배열에서 k=3의 upper bound를 찾는 과정입니다.
1. mid 값을 구하고 k 값과 비교합니다.
- mid = (left + right)/2 = (0 + 9)/2 = 4
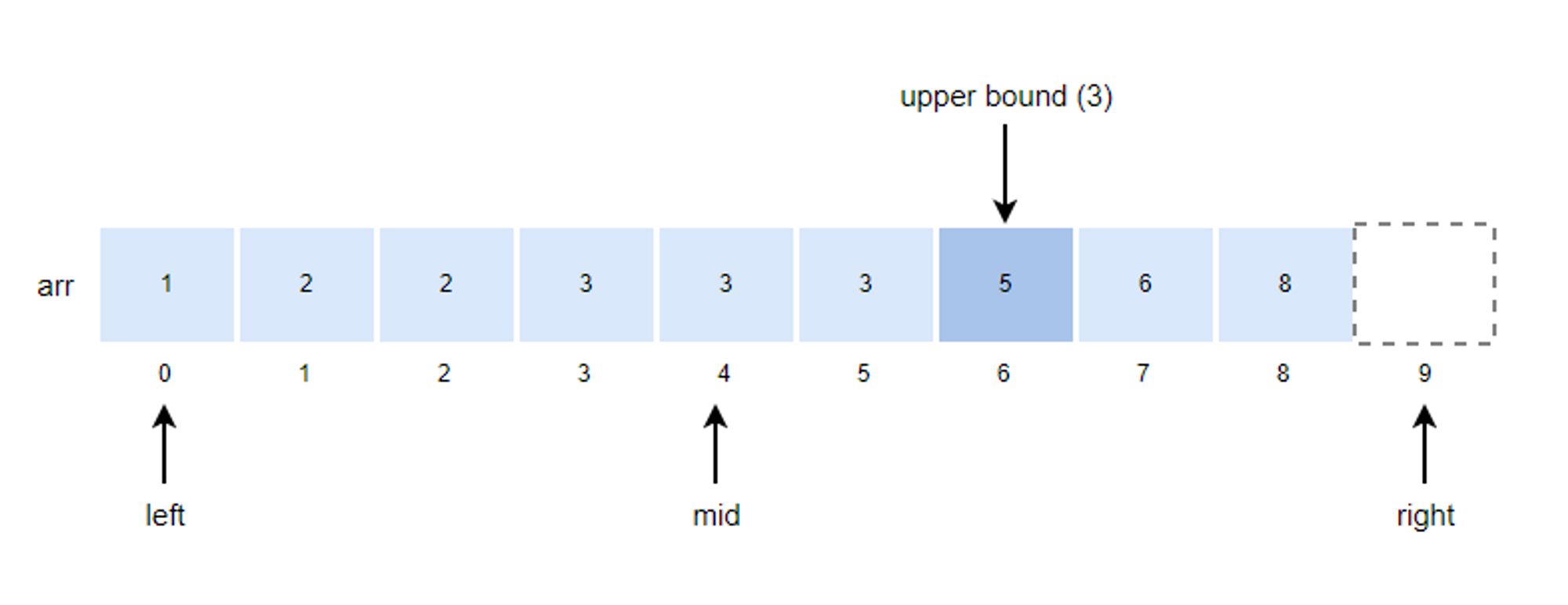
2. k값이 arr[mid]값과 같기 때문에 left의 위치를 mid+1로 변경합니다.
- left = mid + 1 = 4 + 1 = 5
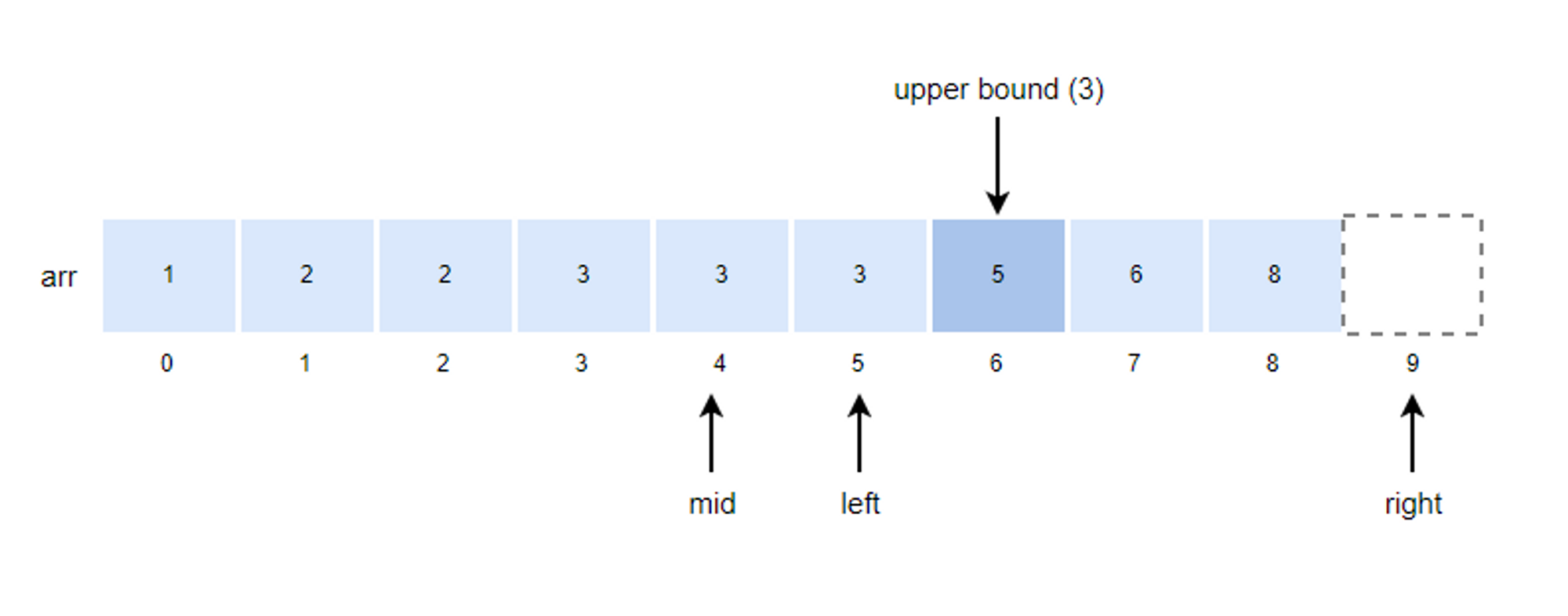
3. mid 값을 구하고 k 값과 비교합니다.
- mid = (left + right)/2 = (5 + 9)/2 = 7
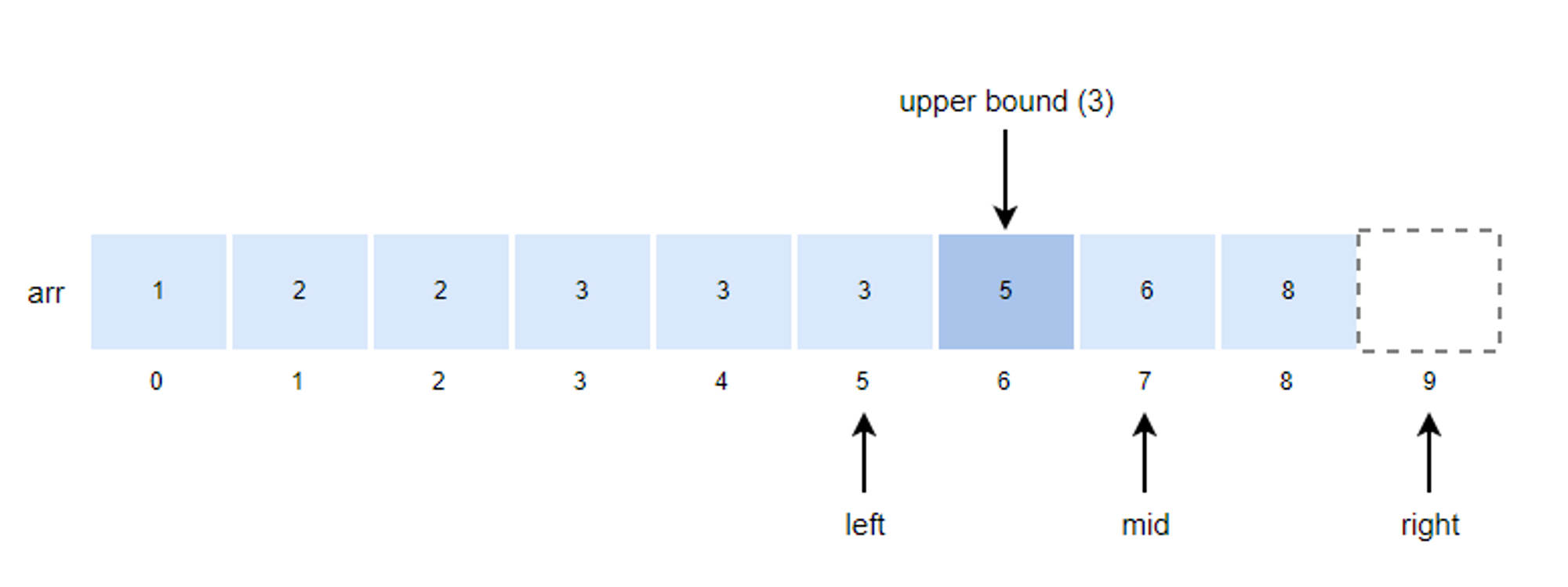
4. k값이 arr[mid]값보다 작기 때문에 right의 위치를 mid로 변경합니다.
- right = mid = 7
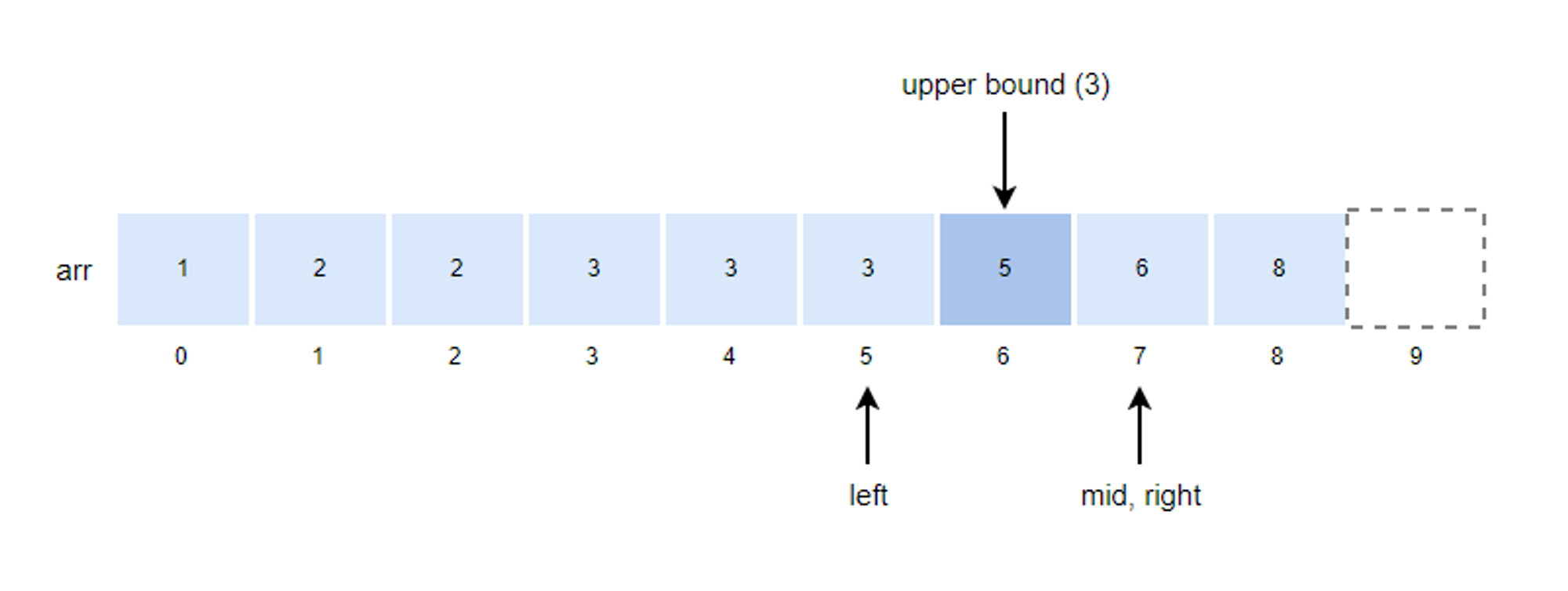
5. mid 값을 구하고 k 값과 비교합니다.
- mid = (left + right)/2 = (5 + 7)/2 = 6
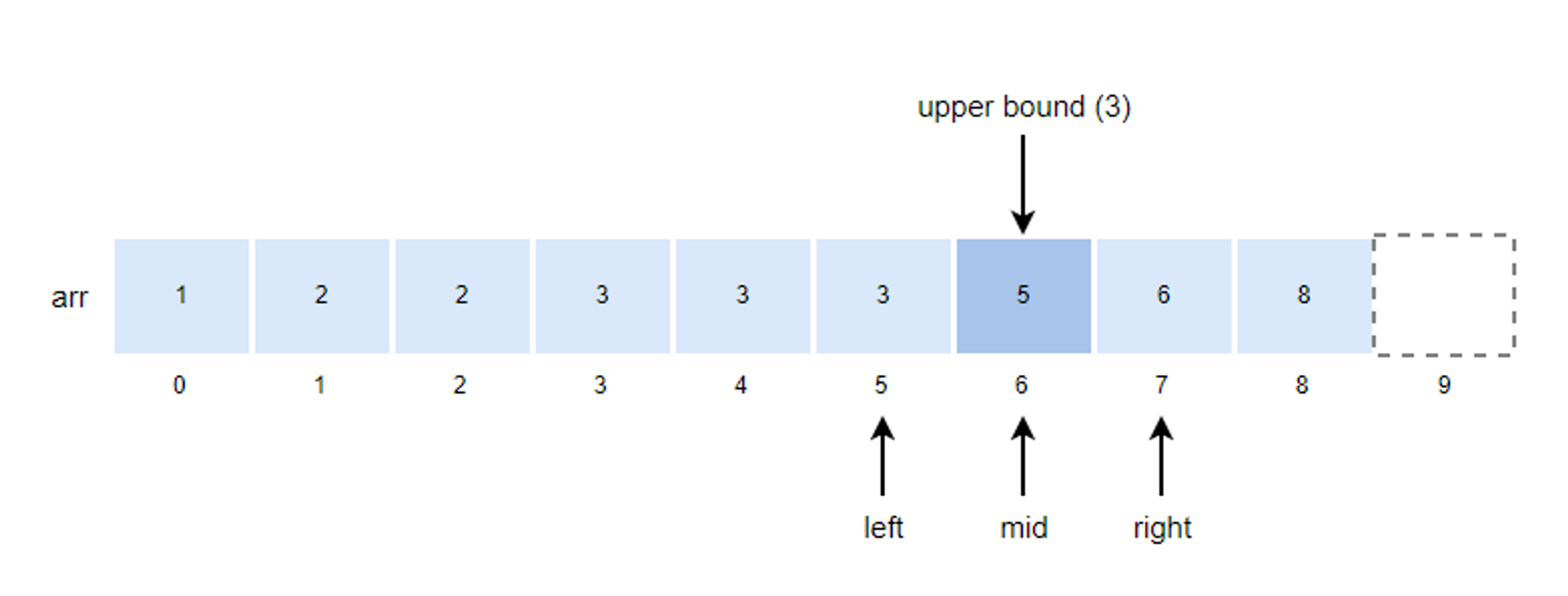
6. k값이 arr[mid]값보다 작기 때문에 right의 위치를 mid로 변경합니다.
- right = mid = 6
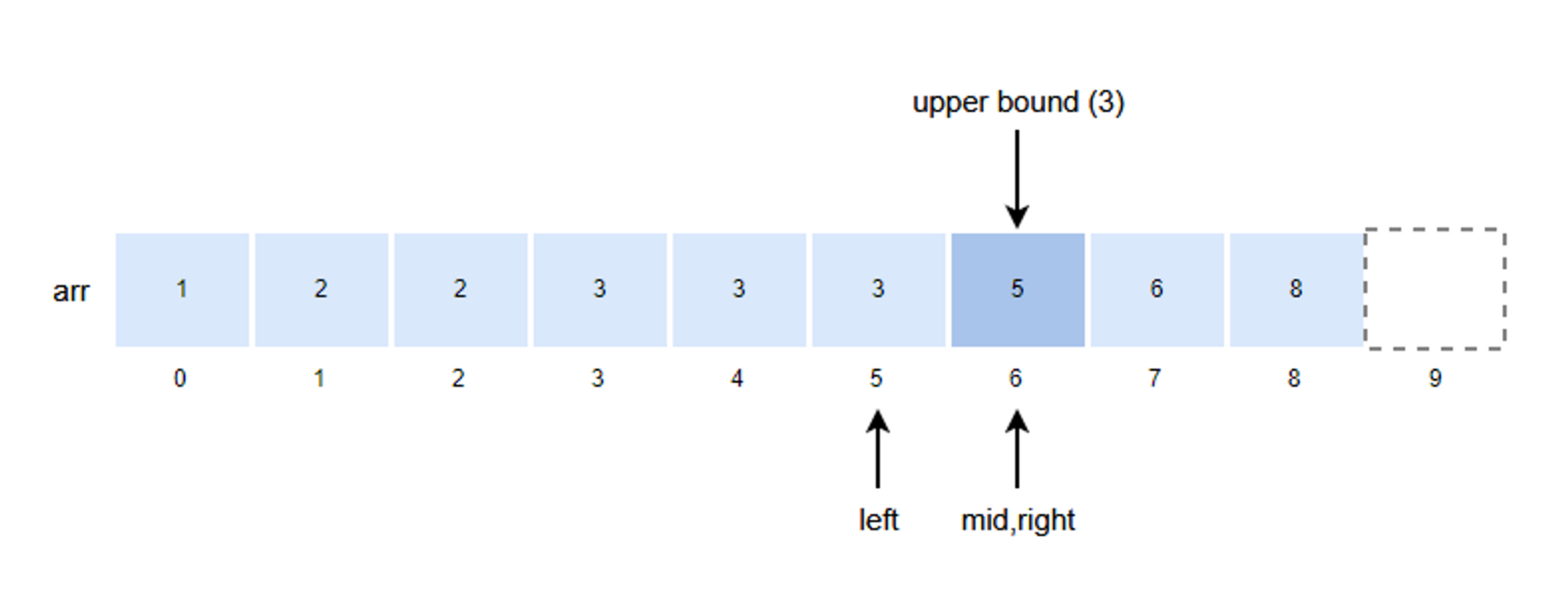
7. mid 값을 구하고 k 값과 비교합니다.
- mid = (left + right)/2 = (5 + 6) / 2 = 5
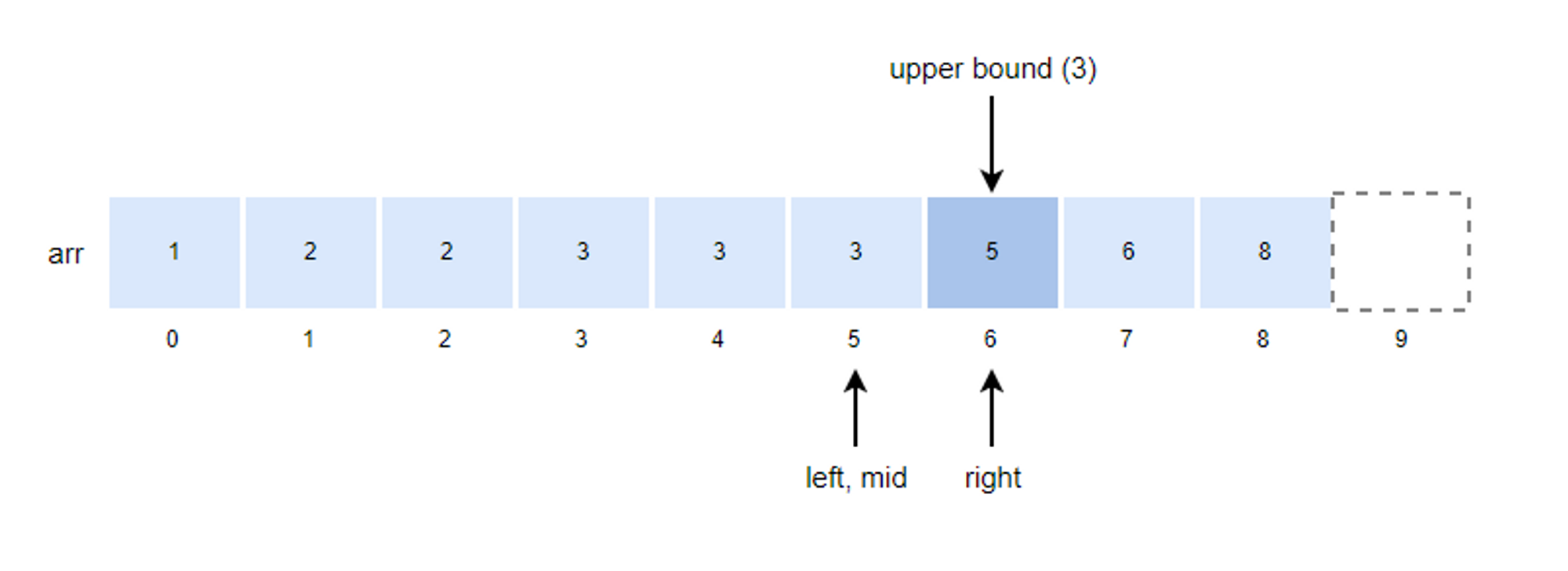
8. k값이 arr[mid]값과 같기 때문에 left의 위치를 mid+1로 변경합니다.
- left = mid + 1 = 5 + 1 = 6
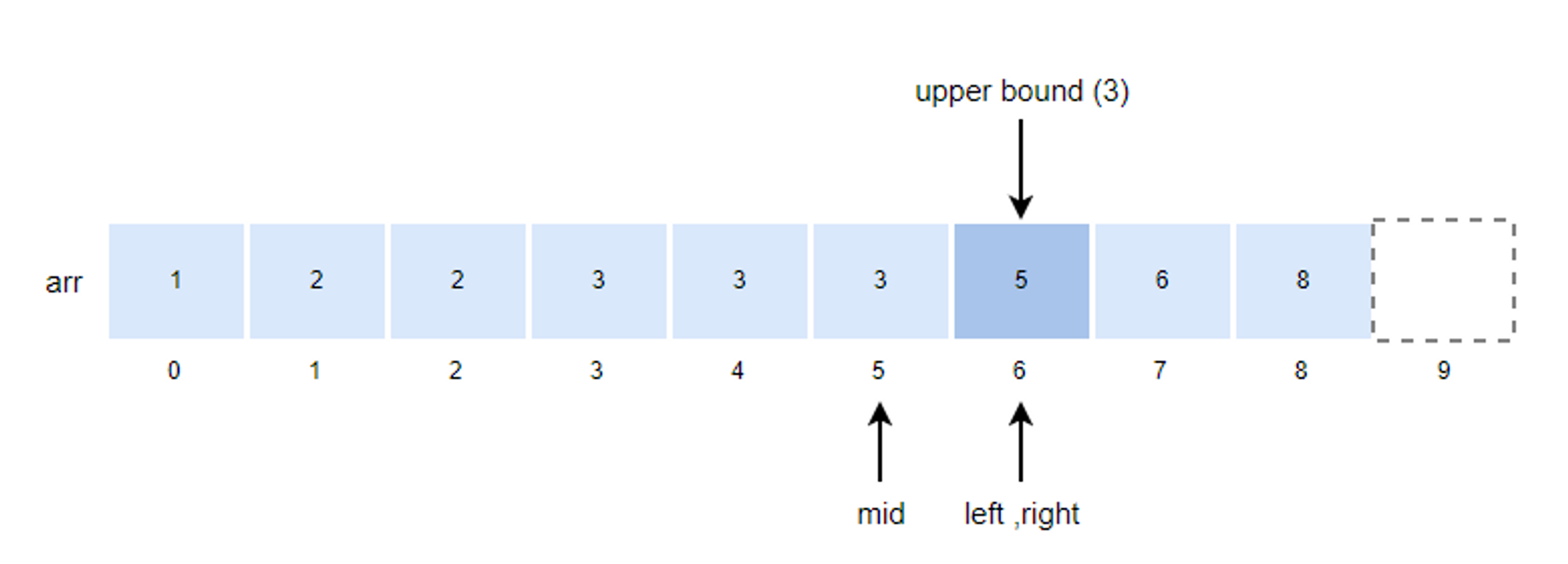
- left값이 right값과 같기 때문에 루프를 종료하고 right값이 upper bound 값이 됩니다.
구현
다음은 arr배열에서 k값의 upper bound를 찾는 코드입니다.
- 매개변수로 left는 배열의 시작위치 right는 arr의 길이로 받습니다.
def upper_bound(arr, left, right, k):
while left < right:
mid = (left + right)//2
if arr[mid] <= k:
left = mid + 1
else:
right = mid
return right