보간 탐색 (Interpolation Search) 개념 및 구현
보간 탐색 (Interpolation Search)은 정렬된 리스트에서 범위를 줄여가며 검색하는 알고리즘입니다. 보간 검색은 전화부에서 이름 (책의 항목이 정렬되는 키 값)을 검색하는 방법과 유사합니다.
동작 방식은 이진 탐색과 비슷하지만 탐색 위치를 정하는 방식이 다릅니다.
이진 탐색과 보간 탐색의 탐색 위치를 결정하는 공식은 다음과 같습니다.
- arr [] : 데이터가 들어있는 배열
- low : arr [] 배열에 시작 index
- high : arr[] 배열에 마지막 index
- x : 검색 값
- pos : 탐색 위치 index
이진 탐색
\( pos = (low + high) / 2 \)
보간 탐색
\( pos = low + (x - arr [low]) * (high - low) / (arr [high] - arr [low]) \)

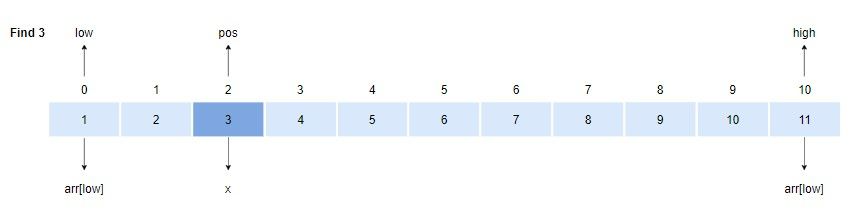
위 그림은 검색 값 3을 찾을 때 첫 번째 탐색 위치를 보여줍니다.
이진 탐색은 항상 중간 위치로 탐색 위치를 결정합니다.
반면에 보간 탐색은 검색키 값에 따라 다른 위치로 이동하게 됩니다. 예를 들어 검색 값이 상대적으로 앞에 있다고 판단하면 앞쪽에서 탐색을 진행합니다.
데이터가 선형으로 분포되어 있으면 위에 그림과 같이 보간 탐색은 한 번에 데이터를 찾기도 합니다.
이처럼 보간 탐색은 데이터가 선형으로 분포되어 있을수록 검색 효율이 좋습니다.
선형으로 분포되어있다는 말은 데이터가 인덱스 값에 비례한다는 의미입니다.
탐색 위치 공식 유도
보간 탐색은 데이터가 선형으로 분포되어 있다고 가정합니다.
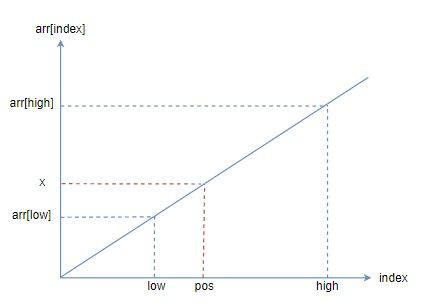
직선의 방정식 : \(y = m*x + c \)
y는 배열에 있는 값이고 x는 배열의 인덱스, m은 직선의 기울기입니다.
직선의 방정식에 low, pos, high를 대입하면 다음과 같습니다.
\( arr [high] = m*high + c \) ... 1
\( arr [low] = m*low + c \) ... 2
\( x = m*pos + c \)... 3
\( m = (arr[high]-arr [low])/(high-low) \)
3번 공식에 2번을 대입하면 다음과 같습니다.
\( x = m*pos + arr[low] - m*low \)
\( m*pos = m*low + x - arr[low] \)
\( pos = low + (x-arr [low])/m \)
마지막으로 m 값을 대입하면 탐색 위치를 구하는 공식이 됩니다.
$$pos = low + (x-arr[low])*(high-low)/(arr[high] - arr[low])$$
동작 방식
보간 탐색은 정렬된 배열에서만 사용할 수 있고 이진 탐색과 동작 방식은 같습니다.
- 탐색 위치(pos)를 가져옵니다.
- 탐색 위치에 있는 값과 검색 값을 비교합니다.
- 값이 같다면(arr[pos] == key) 종료합니다.
- 검색 값이 크다면(arr[pos] < key) 탐색 위치 기준 배열의 오른쪽 구간을 대상으로 탐색합니다. (low = pos+1)
- 검색 값이 작다면(arr[pos] > key) 탐색 위치 기준 배열의 왼쪽 구간을 대상으로 탐색합니다. (high = pos-1)
- 값을 찾거나 간격이 비어있을 때까지 반복합니다.
검색 예
보간 탐색을 사용하여 x = 32 값을 찾는 과정을 보도록 하겠습니다.
1. 탐색 위치 pos를 구합니다.
\(pos = low + (x-arr[low])*(high-low)/(arr[high] - arr[low]) \)
\( = 0 + (32 - 5) *(9-0)/(60-5) = 4.42 = 4 \)
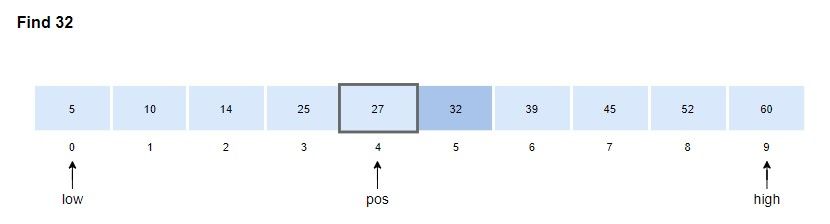
2. arr[pos]와 검색 값을 비교합니다.
- arr[pos] < x 이므로 배열의 오른쪽 구간을 검색 범위로 정합니다.
\( low = pos + 1 = 4 + 1 = 5 \)
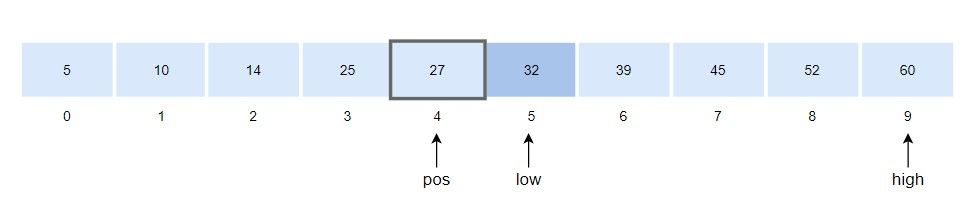
3. 탐색 위치 pos를 구합니다.
\(pos = low + (x-arr[low])*(high-low)/(arr[high] - arr[low]) \)
\( = 5 + (32 - 32)*(9-5)/(60-32) = 5 \)
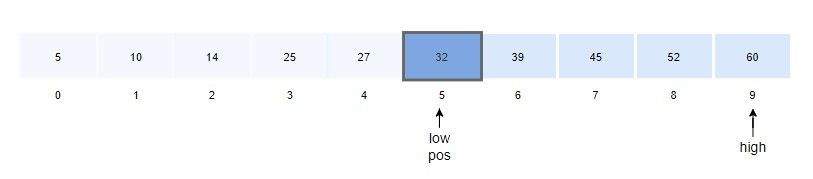
4. arr[pos]와 검색 값을 비교합니다.
- arr[pos] == x 이므로 탐색을 종료합니다.
종료 조건
보간 탐색의 종료 조건은 두 가지가 있습니다. 다음 조건중 하나라도 성립하면 검색을 종료합니다.
1. 검색을 성공할 경우
- 검색 값을 발견한 경우
- a[pos] == key
2. 검색을 실패한 경우
- 검색 범위를 벗어날 경우
- x < arr[low] && x > arr[high]
구현
위 종료 조건을 가지고 구현을 해보겠습니다.
int interpolationSearch(int arr[], int n, int x)
{
int low = 0, high = (n - 1);
int pos = 0;
while (arr[low] != arr[high] && x >= arr[low] && x <= arr[high])
{
pos = low + (((double)(high - low) / (arr[high] - arr[low])) * (x - arr[low]));
if (arr[pos] == x)
return pos;
else if (arr[pos] > x)
high = pos - 1;
else
low = pos + 1;
}
if (x == arr[low])
return low;
else
return -1;
}- 탐색 위치(pos)를 구할 때 값에 오차를 줄이고자 실수 연산을 합니다.
- arr[low] == arr[high] 일 때 pos 값은 low입니다.
- pos값을 구하는 연산 비용을 줄이기 위해 arr[low] != arr[high] 조건을 추가하고 반복문을 벗어나면 x값과 arr[low]값을 비교하는 로직을 추가하였습니다.
시간 복잡도
보간 탐색은 데이터가 선형적으로 균등하게 분포되어 있을 경우 평균 O(log(log n))에 시간이 걸리지만 최악의 경우 데이터가 기하급수적으로 늘어난다면 O(n)에 시간이 걸리게 됩니다.
| Operation | Best | Average | Worst |
| Search | O(1) | Θ(log(log n)) | O(n) |
*n = 데이터 수




